RDP 9307: Explaining Forward Discount Bias: Is it Anchoring? 2. Irrational Agents, Anchoring and Foreign Exchange Puzzles

The idea that irrational market participants exert an influence on market prices dates back a long time (for example, see Mackay (1841) on the seventeenth century tulipmania). But the stage was set for modern discussion of this issue by the debate between Nurske (1944) and Friedman (1953) about the importance of destabilizing speculation in the foreign exchange market. Recent interest in the relevance of irrational market participants has been spurred by evidence of ‘excess volatility’ in financial markets (LeRoy and Porter (1981), Shiller (1989)), by price movements which seem hard to reconcile with the efficient markets model (like the 1987 stockmarket crash or the aerobatics of the $US in the 1980s) and by formal analysis of fads, fashions and ‘noise traders’ in financial markets (Kyle (1985), Summers (1986), Black (1986), Shiller (1989), De Long et. al. (1990a), (1990b), (1991) and Campbell and Kyle (1993)).

Formal analysis of irrational market agents is usually motivated by an appeal to anecdotal and/or psychological evidence. While this evidence is strongly suggestive, it often relates only loosely to the specification chosen for the irrational agents' behaviour. For example, De Long et. al.'s (1990a) noise trader is characterized by his ‘bullishness’ about the return on a risky asset. But the stochastic properties of this bullishness are chosen for tractability and simplicity, rather than to conform closely to any body of evidence on how people actually behave. A similar comment applies to Frankel and Froot's (1990a) analysis of the swings in the $US in the 1980s. As they point out, the expectations formed by their ‘chartists’ and ‘fundamentalists’ are chosen for simplicity rather than realism.

In this paper, we attempt to take a body of psychological evidence seriously and to base the behaviour of our irrational agents as closely as possible on this evidence. We now review the psychological evidence that ‘anchoring’ is a common, robust and systematic behaviour pattern.

2.1 Anchoring

‘In many [uncertain] situations, people make estimates by starting from an initial value that is adjusted to yield the final answer. The initial value, or starting point, may be suggested by the formulation of the problem, or it may be the result of a partial computation. In either case, adjustments are typically insufficient. That is, different starting points yield different estimates, which are biased toward the initial values. We call this phenomenon anchoring.’ (Tversky and Kahneman (1974), p. 1128, italics added).

Anchoring is a well-established behaviour pattern. The following experiment provides a stark example. A random number between 0 and 100 is generated by spinning a wheel of fortune in the subject's presence and s/he is asked to indicate if this number is higher or lower than the percentage of African countries in the UN. Then, s/he is asked to estimate this percentage. The median estimates of the percentage of African countries in the UN are 25 and 45 for groups that received 10 and 65, respectively, as (random) starting points. Payoffs for accuracy do not reduce the anchoring effect (Tversky and Kahneman (1974)).

While striking, this example prompts an obvious question: is anchoring also observed when subjects are knowledgeable about and familiar with the quantity they are estimating? The evidence of Wright and Anderson (1989) suggests that it is. In an experiment with undergraduate business school students, anchoring remained strong even when the students were asked to estimate quantities about which they had considerable knowledge and experience – like the grade point average of a randomly selected student in their program. Wright and Anderson's study also corroborates the earlier evidence that anchoring remains pronounced even when payoffs for accuracy are provided.

Perhaps most telling for our purposes is an example of anchoring in an information-rich, real-world setting (Northcraft and Neale (1987)). Subjects, who were either undergraduate business school students or professional real estate agents, were given a 10-page packet of information about a house currently for sale. The packet included all the information which local real estate agents claimed might be used to evaluate a piece of residential property. The information was all correct, with the exception of the seller's asking price for the house (which differed from one subject to the next and which, it was hypothesised, might act as an anchor for subjects' estimates of the house's value). Subjects visited the house and its neighbourhood and then provided four estimates of its value (its appraised value; an appropriate advertised selling price; a reasonable price to pay for it and the lowest offer they would accept if they were the seller). For both amateurs and experts, the seller's asking price was a highly significant anchor for each of the estimates of the value of the house.^[5]

As these examples imply, the forward exchange rate fits very closely psychologists' definition of an anchor for expectations of the future exchange rate. After all, the forward rate is the rate at which foreign exchange can be traded today for delivery at a particular future date. Thus there is a clear connection (‘suggested by the formulation of the problem’) between the forward rate and the value of the exchange rate at that future date.

Before explaining our model of anchored foreign exchange traders, we describe the foreign exchange market puzzles on which we focus.

2.2 Foreign Exchange Market Puzzles

The standard test for forward discount bias is the regression:

where Δs_t+k is the change in the log spot price of foreign exchange over the next k periods, fd_t,k is the current k-period forward discount (log of the current k-period forward exchange rate minus log of the spot rate) and u_t+k is a mean-zero error term. Ignoring transaction costs, the null hypothesis that market participants are risk-neutral and rational implies that b = 1.^[6] However, when equation (1) is estimated for exchange rates between OECD economies with comparable inflation rates and for k values up to about 12 months, the overwhelming empirical finding is that b < 1 and often that b < 0.^[7]

There is a stark contrast between these estimates of b and estimates of the coefficient on the forward discount, d, from the regression

where is the average exchange rate change expected by market participants over the next k periods. When equation (2) is estimated under the conditions described above for equation (1), the overwhelming empirical finding is that d > 0 and often that d is insignificantly different from one.^[8] Taken together, equations (1) and (2) imply that with the empirical evidence strongly suggesting that b − d ≠ 0. Thus, there is time t information, fd_t,k which helps to predict the time (t+k) prediction error, s_t+k – . As has been repeatedly stressed, the average survey expectations are not rational expectations.

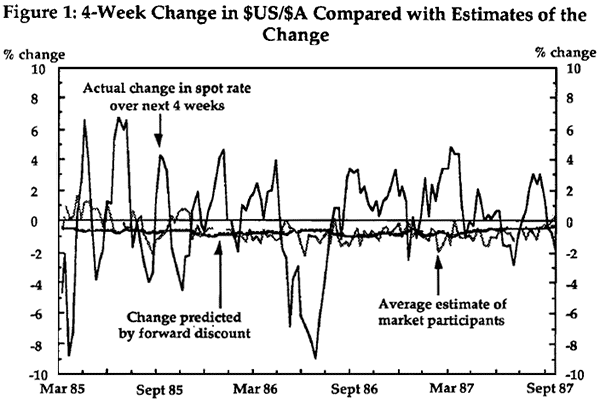
Figure 1 shows exchange rate and expectations data which provide an example of these puzzles.^[9] Two things stand out. First, it does appear from the figure that the average exchange rate change expected by market participants is correlated with the forward discount, an appearance supported by regression analysis (though the significance level is not high). Second, there is so much exchange rate volatility that it is not obvious from the figure that the forward discount or average market participants' expectations are biased estimates of the future exchange rate change, despite the formal statistical analysis which strongly suggests that they are. Compared to the range of possible outcomes for the actual exchange rate change, the average bias of market participants' expectations is very small.

Figure 1 does not show the substantial heterogeneity in market expectations (Frankel and Froot (1990b), Ito (1990), Takagi (1991)). To give an example from another market, the standard deviation of market participants' expectations of the one-month change in the ¥/$US is 2.2% (Frankel and Froot (1990b)). That is a big number.^[10] At any given time, different market participants have widely different exchange rate expectations. Only when these heterogeneous expectations are averaged over many participants and over a time span measured in years does it become apparent that, on average, market participants' expectations are biased. But as we have said, this average bias is very small.

Where does this small bias come from? For reasons explained above, we assume that some market participants are influenced by the value of the forward rate when forming their exchange rate expectations. In the rest of the paper, we maintain the convenient fiction that there are only two possible types of market participants (traders), rational and anchored, and that all traders of a given type are identical.

Footnotes

However, the experts seemed much less aware that they were being influenced by the anchor! When asked what factors had influenced their valuations, 56% of the amateurs mentioned the asking price, while only 24% of the experts did. [5]

a = 0 is also sometimes included as part of the null, although it is not a general implication of risk-neutrality and rational expectations. Different assumed distributions of exchange rate changes imply different values for a because of Jensen's inequality (see, for example, Frankel (1983)). [6]

To give two representative examples, Goodhart (1988) estimates equation (1) for nine datasets over time periods ranging from 1974–1980 to 1974–1986. He examines the £, DM, Swfr and ¥ all against the $US, and studies both k = one month and k = three months. In six cases out of nine the point estimate of b is negative, and in five cases it is significantly (more than two standard errors) less than one. By contrast, in no case can he reject the null hypothesis that b = 0. Frankel and Chinn (1991) report pooled time series/cross section regressions of equation (1) for the exchange rates of 17 countries against the US using k = three months over the time period February 1988 – February 1991. (They also report qualitatively similar results for k = 12 months.) The point estimate (GMM standard error) of b is b = −0.67 (0.41) when the constant term, a, is constrained to be equal across countries and b = −2.88 (0.65) when it is unconstrained. [7]

is derived from surveys of market participants. To reduce the effect of outliers on the results, it is often the harmonic mean or the median of the survey responses, rather than the arithmetic mean. We assume that the surveys truly reflect average market expectations (at least up to a random measurement error). Froot and Frankel (1989) estimate equation (2) for a range of survey datasets. In seven cases out of nine, they accept the hypothesis that d = 1 and conclude (p. 149) that: ‘Expectations seem to move very strongly with the forward rate.’ They also find that the point estimates of b in equation (1) for the time periods of their survey data are usually negative and statistically significantly less than 1. Frankel and Chinn (1991) report pooled time series/cross section regressions of equation (2) for survey data corresponding to the exchange rates and time period quoted in footnote 7. The point estimate (GMM standard error) of d for a 3-month horizon is d = 0.82 (0.18) when c is constrained to be equal across countries and d = 0.42 (0.20) when c is unconstrained. [8]

For these data, Δs_t+k = −0.04 (0.02) – 6.2 (3.1) fd_t,k ; = 0.0 (0.005) + 1.2 (0.7) fd_t,k with k = 4 weeks and GMM standard errors in parentheses (Smith and Gruen (1989)). [9]

The average one-month change in the ¥/$US is about 0.2% while its standard deviation is 3.2%. The former number is an average from 1974 to 1990; the latter is from Baille and Bollerslev (1989). [10]