RDP 9706: Is the Phillips Curve A Curve? Some Evidence and Implications for Australia Appendix A: The Kalman Filter

In order to execute the Kalman filter, the following information needs to be provided to the model:

1. β₀, the initial values of the state vector;
2. the initial covariance matrix of β;
3. the variance of the measurement equation (variance of ε_t); and
4. the variance of the transition vector (variance of μ_t).

Note that if Q, H and Σ_t are all multiplied by a constant, the constant does not affect estimates of the state-space vector β. It is only the ratio between the variances that affects the estimates of β. A usual procedure is to normalise H = 1. This procedure is followed below.

The elements in Σ₀ are set to relatively large values, reflecting lack of knowledge about the covariance between elements of the state space equation. Q is a 3x3 matrix (because there are three elements in the state vector), however it has only one non-zero element, because only the second element of β_t is time-varying. This value, as well as the three initial values for the coefficients in β_t, are estimated using a non-linear maximum-likelihood optimisation procedure. We estimated starting values for the model parameters using a numerical optimisation procedure in RATS, which chooses these values by maximising a concentrated log-likelihood function.^[19] This exercise was tractable because of the parsimonious model specification used.

Footnote

The form of the likelihood function used is 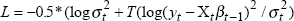. See Doan (1992) for more details. [19]