Appendix B: Further Estimation Results | RDP 9706 Is the Phillips Curve A Curve? Some Evidence and Implications for Australia

RDP 9706: Is the Phillips Curve A Curve? Some Evidence and Implications for Australia Appendix B: Further Estimation Results

Guy Debelle, James Vickery

October 1997

Table B.1: Adaptive Expectations
Phillips curve:

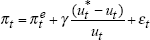where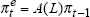
γ	LLF	σ²	α	max[u-u^*]	max[Δu^*]
1.26	11.58	0.93	0.95	4.93	1.05
(3.55)
(2.10)
Phillips line:

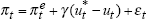where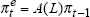
γ	LLF	σ²	α	max[u-u^*]	max[Δu^*]
0.40	24.48	0.21	0	8.00	4.27
(2.11)
(3.14)
t-statistics in parentheses: unadjusted, and Newey-West corrected
γ	labour-market sensitivity parameter
LLF	value of the log-likelihood function
σ²	standard error of the equation
α	average value of u-u^*

Table B.2: Melbourne Institute Expectations
Phillips curve:

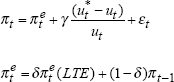γ	δ	LLF	σ²	α	max[u-u^*]	max[Δu^*]
1.15	0.09	1.90	0.31	1.54	6.73	0.67
(2.67)	(1.97)
(1.75)	(1.23)
Phillips line:

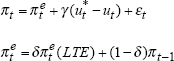γ	δ	LLF	σ²	α	max[u-u^*]	max[Δu^*]
0.27	0.07	6.30	0.10	0	3.56	1.72
(1.26)	(0.90)
(2.95)	(0.90)
t-statistics in parentheses: unadjusted, and Newey-West corrected
γ	labour-market sensitivity parameter
δ	weight given to forward-looking component of inflation expectations
LLF	value of the log-likelihood function
σ²	standard error of the equation
α	average value of u-u^*
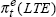	forward-looking inflation expectations based on the Melbourne Institute survey of inflation expectations
Note: There is an extremely large amount of variation in the NAIRU under both the linear and non-linear model in the early part of the sample. Figures quoted here for α, max[u-u] and max Δu exclude observations from the first three years of the sample for which the Melbourne Institute survey was available (1973 to 1975).

Table B.3: Model with Speed Limits
Phillips curve:

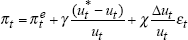where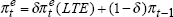
γ	δ	χ	LLF	σ²	α	max[u-u^*]	max[Δu^*]
1.43	0.11	1.86	19.80	0.46	1.22	6.08	1.24
(3.45)	(2.95)	(2.31)
(3.32)	(2.16)	(0.810)
Phillips line:

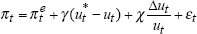where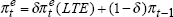
γ	δ	χ	LLF	σ²	α	max[u-u^*]	max[Δu^*]
0.31	0.18	1.53	29.99	0.16	0	7.41	3.43
(1.56)	(2.36)	(1.59)
(4.02)	(2.84)	(0.71)
t-statistics in parentheses: unadjusted, and Newey-West corrected
γ	labour-market sensitivity parameter
δ	weight given to forward-looking component of inflation expectations
χ	parameter on speed limit term
LLF	value of the log-likelihood function
σ²	standard error of the equation
α	average value of u-u^*
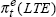	forward-looking inflation expectations based on bond yields, equal to the 10-year bond rate less the world real interest rate

Table B.4: Model with Dummy Variables
Phillips curve:

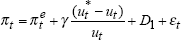where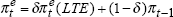
γ	δ	D₁	LLF	σ²	α	max[u-u^*]	max[Δu^*]
0.94	0.13	2.59	36.82	0.35	2.10	7.89	1.33
(2.28)	(3.65)	(4.85)
(4.22)	(2.41)	(2.28)
Phillips line:

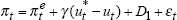where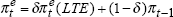
γ	δ	D₁	LLF	σ²	α	max[u-u^*]	max[Δu^*]
0.20	0.18	2.20	39.21	0.14	0	6.80	5.69
(1.00)	(2.33)	(2.89)
(3.81)	(3.73)	(2.44)
t-statistics in parentheses: unadjusted, and Newey-West corrected
γ	labour-market sensitivity parameter
δ	weight given to forward-looking component of inflation expectations
D₁	dummy variable for the period 1973:Q3–1975:Q2
LLF	value of the log-likelihood function
σ²	standard error of the equation
α	average value of u-u^*
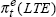	forward-looking inflation expectations based on bond yields, equal to the 10-year bond rate less the world real interest rate