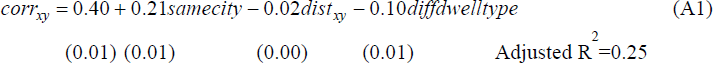RDP 2006-04: Measuring Housing Price Growth – Using Stratification to Improve Median-based Measures Appendix A: Using the Information in Individual Strata – Assessing the Strength of Intra-versus Inter-state Influences
May 2006
- Download the Paper 233KB
Although the proposed new measure of price changes was designed to look at house prices on an aggregate city-wide level, the price movements in the individual strata may also be of interest in answering questions about the behaviour of house prices in different segments of the market. Accordingly, we briefly consider the extent to which price movements in a particular segment of a capital city market, as proxied by the median price of each decile (quintile), are correlated with price movements of other market segments. Since our strata are defined in terms of average prices for suburbs, they correspond to economic segments (e.g. the ‘higher end’ and the ‘lower end’ of the market) rather than regional segments (e.g. the inner or outer suburbs).
The average correlation coefficient between year-ended price changes in strata medians across capital cities is 0.52, compared with an average correlation coefficient of 0.79 for strata medians within the same capital city. The first of these numbers points to a reasonable amount of co-movement in housing price growth across different cities, suggesting the existence of a national housing cycle. This is not surprising given that state business cycles are highly correlated and the presence of many common national influences.[23] However, within-city correlations tend to be even higher. This suggests the existence of significant regional effects within individual markets.
To more fully examine the relationship of price growth between different market segments, we calculated the correlation coefficients between quarterly changes in median price in the 65 different strata. Using the 2,080 different correlation coefficients, we then estimated a regression to assess what factors are associated with higher correlations between strata. This allows us to test for same-city versus across-city effects in price growth. It also allows us to test if there is any tendency for some degree of segmentation between the markets for houses and apartments and if higher-price strata tend to be more correlated with other higher-price strata, and vice versa. To test the latter effect, we define the economic ‘distance’ between two strata as the absolute magnitude of the difference between the decile rankings of two strata. For example, the distance variable between decile 6 in Sydney and decile 8 in Perth would be 2.[24] If we find that strata which are economically relatively ‘close’ to each other tend to have higher correlations, this might be evidence for the existence of factors working on a national level that have differential effects on the higher-and lower-end of the nationwide property market.
We obtain the following regression result:
where: corrxy refers to the correlation coefficient between median quarterly price movements in strata x and y (where x≠y); samecity is a dummy variable which is equal to 1 if x and y are in the same city (and 0 otherwise); distxy refers to ‘economic distance’ between two strata, as defined above; and diffdwelltype is a dummy variable taking the value of 1 if x and y refer to different types of dwellings. Heteroskedasticity-consistent standard errors are shown in parentheses below the parameter estimates.[25]
The results are as expected. The significant constant term suggests a noticeable co-movement in price growth across different segments of the national market, with its value of 0.40 indicating the average correlation between quarterly price movements in two strata that are in different cities, of the same dwelling type, and in the same economic segments (zero distance). The most important variable for explaining differences in the strength of correlations is whether or not the two strata are in the same city, with this variable explaining around half of the fit of Equation (A1).
The results also show that price movements are less correlated the greater the economic distance between the two strata. This provides evidence of socio-economic factors on a national level that have different impacts on price growth in higher-and lower-priced suburbs. In addition, the results show a higher correlation in price movements within dwelling types as opposed to across dwelling types, suggesting that there may be factors which tend to affect nationwide house prices more than apartment prices, or vice versa. This could be additional evidence of some type of common socio-economic effects, as household type tends to differ across dwelling types.[26]
Overall, the results suggest that there is a reasonably high degree of correlation in movements in dwelling prices across segments of the Australian housing market, especially in cases where there is a higher degree of similarity between two market segments in terms of location, dwelling type and ‘economic background’.
Footnotes
Norman and Walker (2004) find a significant degree of co-movement across state business cycles, with the major source of cyclical fluctuations in state cycles arising from shocks that are common to all states. [23]
In the case of quintiles, we number quintiles by the midpoint of two corresponding deciles: for example, quintile 1 is considered to be decile 1.5, quintile 2 would be 3.5 and so on. [24]
For ease of understanding, we show results using ordinary least squares (OLS). OLS may not be the most appropriate estimator for this equation, given that the dependent variable is bounded by 1 and −1. However, similar results hold when we run the regression using the Fisher z transformation which can be used to transform the correlation coefficients into normally distributed variables. An additional economic problem may result because as the 2,080 observations come from only 65 data series, this may bias the standard errors downwards. [25]
In other work, we have also used Granger causality tests to look for the existence of any systematic lead-lag relationship between the higher-and lower-priced segments of the market. The results differ across cities, with some cities suggesting Granger causality from the high end to the low end, other cities suggesting the opposite, and others suggesting either no causality or causality running in both directions. Overall, it appears there is no systematic lead-lag relationship; rather, there is a high degree of contemporaneous correlation between price movements in the higher-and lower-priced segments in each city. [26]