RDP 2006-04: Measuring Housing Price Growth – Using Stratification to Improve Median-based Measures 5. Assessing the Mix-adjusted Median
May 2006
- Download the Paper 233KB
We assess our alternative measure of changes in city-wide house prices by examining how well it addresses the problems with conventional unstratified median measures that were highlighted in Section 2. An additional benchmark is whether our measures outperform the change in the seasonally adjusted median price: this will indicate if the slightly greater data demands of our measure yields a significant improvement relative to a simple alternative approach to dealing with the problem of seasonality and compositional change. In addition, we also compare the correlation of our measure with regression-based measures. We then provide some additional perspective on the reasons for the good performance of our simple measure.
5.1 Volatility
Price movements that result from compositional effects can be considered as representing noise that adds volatility to quarterly price changes rather than being indicative of true trends in the housing market. Indeed, the results in Panel A of Table 4 indicate that quarterly changes in median housing prices in Australian cities are highly volatile.[16] In every case, simply seasonally adjusting the median price series (using the X12 program) results in a measure of price changes that is considerably less volatile than the change in the unadjusted median. However, in every case there is an additional improvement that can be gained from our simple mix-adjusted measure.
| Median (nsa) | Median (sa) | Mix-adjusted measure | Range for deciles/quintiles (nsa) | |
|---|---|---|---|---|
| Panel A: Standard deviation of quarterly changes | ||||
| Sydney houses | 4.35 | 3.30 | 2.16 | 2.36–3.61 |
| Melbourne houses | 4.62 | 3.00 | 2.26 | 2.24–3.86 |
| Brisbane houses | 3.10 | 2.92 | 2.92 | 2.92–5.21 |
| Perth houses | 2.29 | 1.98 | 1.80 | 2.46–3.62 |
| Adelaide houses | 2.90 | 2.36 | 2.27 | 2.73–6.17 |
| Canberra houses | 3.51 | 3.44 | 3.06 | 3.57–5.12 |
| Sydney apartments | 2.27 | 1.87 | 1.84 | 2.17–3.18 |
| Melbourne apartments | 3.87 | 3.50 | 2.70 | 3.36–5.73 |
| Australian housing | 3.13 | 2.25 | 1.81 | |
| Panel B: Deviation from trend (quarterly RMSE) | ||||
| Sydney houses | 4.04 | 2.80 | 1.08 | 1.41–2.99 |
| Melbourne houses | 4.40 | 2.54 | 1.40 | 1.36–3.48 |
| Brisbane houses | 1.91 | 1.61 | 1.26 | 1.73–4.88 |
| Perth houses | 1.90 | 1.49 | 1.07 | 1.73–3.10 |
| Adelaide houses | 2.20 | 1.37 | 1.27 | 1.71–6.07 |
| Canberra houses | 2.46 | 2.41 | 1.88 | 2.33–4.78 |
| Sydney apartments | 1.93 | 1.46 | 1.21 | 1.60–2.89 |
| Melbourne apartments | 3.45 | 3.01 | 2.11 | 2.78–5.59 |
| Australian housing | 2.81 | 1.73 | 0.88 | |
| Note: The sample covers 1993:Q2–2005:Q3. | ||||
The reduction in volatility between the non-seasonally adjusted median and the mix-adjusted measure is greatest for Sydney and Melbourne houses, where the standard deviation is reduced by half. Indeed, it is noteworthy for Sydney and Melbourne houses that the standard deviation of price changes in every one of the ten deciles is noticeably smaller than the standard deviation of the change in the median for the entire city. To be provocative, these results for Sydney and Melbourne suggest that one might get better estimates of the trend in city-wide house prices by looking at developments in a sample of only about 10 per cent of all sales (albeit a carefully selected 10 per cent) than from a standard median measure using the full sample of data.
The comparisons in Panel A of Table 4 implicitly assume that the amount of ‘noise’ in a series for price changes can be proxied by its standard deviation, that is, by the variability relative to the average change over the entire sample period. An alternative would be to recognise that there are cycles in price movements, so we should assess different series for price changes based on how closely they match a measure of the ‘trend’ change in prices. Accordingly, we construct a moving-average measure of the trend change in prices for each city. For each price measure we then calculate a root mean squared error (RMSE) between quarterly growth in the measure and quarterly growth in the trend.[17] Since the trend measure can be thought of as capturing underlying housing price movements, the larger the deviations from trend, the less informative the series is about the underlying state of the housing market.
The results for the RMSE in Panel B of Table 4 again suggest that a seasonally adjusted median price series offers an improvement over the standard median, but that the mix-adjusted measure provides a more significant improvement for all capital cities. Taking the reduction in the Australia-wide measure as a simple metric for the reduction in the proportion of noise in the standard median, one might conclude that seasonal adjustment can typically reduce the extent of noise by nearly 40 per cent, but that the mix-adjusted measure results in a more significant reduction, with the average volatility falling by nearly 70 per cent.
The reduction in volatility from adjusting for compositional change appears to be significantly greater for houses in Sydney and Melbourne than in the other capitals. The gains from stratification will depend on several factors including: the extent of compositional change between higher-and lower-priced properties in each city; the extent of price differences between higher-and lower-priced properties; and the extent to which we can ‘undo’ the effects of compositional change via the suburb-level stratification strategy used here. We cannot be definitive about the reasons for the relatively larger gains for the larger cities, but they appear to reflect both a higher degree of compositional change in these two cities (including the seasonal component shown in Panel A of Table 2), and greater variation in the characteristics of the dwelling stock in Sydney and Melbourne (for example, the median house price for the tenth decile in Sydney is on average 2.7 times higher than the city-wide median, compared with around 2.2 times higher for most of the other capitals). In addition, since the largest cities have the largest number of suburbs (for example, 659 for Sydney versus 313 for a medium-sized city like Perth), it is possible to divide larger cities into more differentiated strata with greater variation in the average prices of suburbs in each strata. Hence it would be expected that there would be greater gains from stratification and greater control of compositional change in the larger cities.
5.2 Seasonality
By construction, our mix-adjusted measure will remove any impact on measures of price changes that results from seasonality in the composition of sales across strata. However, it will not control for any seasonality from compositional effects within strata. To see if seasonality within strata is an issue, we have tested our measure for the presence of any residual seasonality. While median prices in nearly all capital cities were found to be seasonal, the results (available upon request) indicate that mix-adjusted changes are not seasonal in any capital city, nor at the nationwide level.
Therefore, by controlling for one form of compositional effect through stratification, we are providing a control for the seasonality that is apparent in median measures. In addition to this, it appears that we are also controlling for some degree of non-seasonal compositional change. Accordingly, our measure appears in Table 4 to be a significant improvement over the seasonally adjusted measure.
5.3 Revisions
An additional test of the mix-adjusted methodology is the extent to which it performs well in real time, as opposed to the previous comparisons in this paper which are based on more final data. The real-time data problem is the result of the decentralised nature of the housing market in Australia, which means that information on house prices has often used data from state land titles offices reported only after the settlement of transactions. This means that sales information is often not available until several months after the agreement on the transaction price. Therefore, initial estimates of prices in transactions occurring in any given quarter may be based on only a small sample of all transactions that will eventually be available.
If there are systematic differences in the lag between agreement on a sale and the reporting of the sale, early samples of transactions may be quite unrepresentative of the final population of sales. For example, a simple median will be biased downwards if more expensive houses are under-represented in initial samples. Hence, early estimates of changes in housing prices may be unreliable, making it difficult to discern true movements in the housing market from those that result from small sample size or compositional effects. Indeed, the pattern of upward revisions to real-time estimates of median house prices in most Australian capitals suggest that lower-priced houses are over-represented in initial samples of transactions.[18]
To examine potential problems with early estimates, we use data on individual sales in Sydney, provided by APM, to estimate ‘real-time’ city-wide price growth. We calculate an ‘initial’ estimate of house price growth using data available one month after the end of each quarter and compare this with ‘final’ estimates calculated from the latest available vintage of data; this corresponds to an initial sample that is typically less than half the size of the final sample.[19] A RMSE is then calculated between the ‘initial’ and ‘final’ estimate of price growth for each measure. The results show that the standard median is subject to considerably greater revision (a RMSE of around 7½ percentage points) than the mix-adjusted measure (a RMSE of about 1½ percentage points). Hence, our technique of stratification appears to offer an even greater improvement over a simple median in real time. The improved real-time performance of the mix-adjusted measure is not entirely surprising given that one of the rationales for stratification is that it can reduce the size of a sample required to produce reliable statistics (Briggs and Duoba 2000).
5.4 Comparison with Regression-based Measures
One clear advantage of a mix-adjusted measure is its relative simplicity. However, more sophisticated approaches are possible, most notably the two regression-based measures studied in Hansen (2006). Of course, these approaches are not without shortcomings. For example, hedonic regressions will only be as good as the data on housing characteristics that are available. Repeat-sales estimates are likely to have significant problems in real time and can be subject to non-trivial revisions, given that estimates of price growth in any quarter will be affected by sales that occur in subsequent quarters.
In Table 5, we use correlation coefficients and a measure of deviations from trend to compare our measure and the estimates from Hansen (2006) of quarterly price changes for houses in the three large capitals from hedonic and repeat-sales regressions. Panel A of Table 5 indicates that the change in the simple median often has a fairly modest correlation with the regression-based measures. Seasonal adjustment of the median produces quarterly growth rates that are slightly more correlated with these measures. However, our measure of the quarterly growth in prices is considerably more correlated with the regression-based measures. Indeed, the mix-adjusted measure tends to have a slightly higher correlation with each of the regression-based measures than the correlation between those more advanced measures.
| Median (nsa) | Median (sa) | Mix-adjusted | Hedonic | Repeat-sales | |
|---|---|---|---|---|---|
| Panel A: Correlation coefficients, quarterly changes | |||||
| Sydney | |||||
| Median (nsa) | 1.00 | ||||
| Median (sa) | 0.77 | 1.00 | |||
| Mix-adjusted median | 0.52 | 0.65 | 1.00 | ||
| Hedonic | 0.58 | 0.65 | 0.97 | 1.00 | |
| Repeat-sales | 0.38 | 0.57 | 0.90 | 0.89 | 1.00 |
| Melbourne | |||||
| Median (nsa) | 1.00 | ||||
| Median (sa) | 0.69 | 1.00 | |||
| Mix-adjusted median | 0.65 | 0.71 | 1.00 | ||
| Hedonic | 0.66 | 0.70 | 0.92 | 1.00 | |
| Repeat-sales | 0.42 | 0.57 | 0.76 | 0.69 | 1.00 |
| Brisbane | |||||
| Median (nsa) | 1.00 | ||||
| Median (sa) | 0.95 | 1.00 | |||
| Mix-adjusted median | 0.87 | 0.87 | 1.00 | ||
| Hedonic | 0.89 | 0.90 | 0.96 | 1.00 | |
| Repeat-sales | 0.77 | 0.81 | 0.93 | 0.93 | 1.00 |
| Panel B: Deviation from trend (quarterly RMSE) | |||||
| Sydney | 4.11 | 2.95 | 0.97 | 1.02 | 0.86 |
| Melbourne | 4.48 | 2.64 | 1.40 | 1.25 | 1.57 |
| Brisbane | 1.96 | 1.69 | 1.25 | 1.25 | 1.03 |
|
Notes: Correlation coefficients and RMSEs across the various measures of quarterly price growth were calculated over 1993:Q2–2005:Q3. The data vintage used to calculate the hedonic and repeat-sales measures in Hansen (2006) does not correspond precisely with that used to calculate the mix-adjusted median here. In addition, Hansen uses data from a different source (Real Estate Institute of Victoria) to calculate the repeat-sales measure for Melbourne, so the results across measures are not fully comparable for Melbourne. |
|||||
Panel B indicates the extent to which each of the measures of house price growth deviate from a proxy of underlying house price movements.[20] Confirming the earlier results in Table 4, changes in the median and seasonally adjusted median are volatile with relatively high RMSEs. In contrast, our mix-adjusted measure and the two regression-based measures provide estimates of underlying house price movements that are comparable in terms of their apparent noise.
It is reassuring that the results from the mix-adjusted measure are similar to those from regression-based measures, suggesting that simple stratification techniques can control for a significant proportion of compositional change. However, it is not especially surprising that our measure is highly correlated with the hedonic measures. The results in Hansen (2006) indicate that the vast majority of the explanatory power in standard hedonic regressions comes from the location of properties, which (in combination with information on average suburb-level price levels) is the variable used for stratification in our methodology.
5.5 Why Does the Mix-adjusted Measure Perform Well?
The preceding analysis indicates that the mix-adjusted approach overcomes many of the problems associated with unstratified median measures. A major reason for the substantial improvement appears to be the particular method we have used to stratify transactions. By stratifying properties on the basis of the median price for their suburb, we are controlling for much of the compositional change in sales movements between higher-and lower-priced properties. However, other stratification strategies are possible, an obvious alternative being on a broad geographical basis, which is a common strategy internationally. Accordingly, in this section we compare the results of price-based and geographic stratification strategies.
We use unit record data for Sydney to construct two alternative mix-adjusted measures of price changes. Two standard geographical classifications of Sydney are based on statistical local areas (SLA) and statistical subdivisions (SSD), of which there are 49 and 14 groups respectively. We construct measures using both of these geographic groupings. To produce a city-wide measure of price growth, the median house price in each geographic region is weighted by the region's share of sales over the whole sample period. In order to evaluate the relative performance of the geography-based measures of price growth, we calculate the deviation (RMSE) of each measure from the trend growth series used in Panel B of Table 5.
For greater comparability, we also calculate some alternative price-based mix-adjusted measures. Instead of dividing Sydney into 10 price-based groups, we divide it into 14 and 49 groups (the same number of groups as the geographic measures) based on the median price of that suburb over 2000–2004. However, to shed further light on the stratification issue, we implement some additional price-based measures. In particular, instead of forming measures based just on 10, 14 and 49 strata, we assess the robustness of price-based measures using everything from 1 stratum (equivalent to the simple city-wide median) all the way up to 60 strata (each with just 10 or 11 suburbs).
The results are shown in Figure 4.[21] A first point to note is that price changes estimated from the geographic-based stratifications are less noisy than the simple city-wide median. The RMSEs based on the 14 and 49 groups are 1.95 and 1.62 per cent respectively, versus 4.70 per cent for the city-wide median. However, the price-based stratification measures provide a significant additional improvement over the geography-based measures, with RMSEs of 1.15 and 1.14 per cent, respectively, for the measures based on 14 and 49 groups. This provides evidence in support of grouping data on the basis of median suburb prices rather than on a geographic basis, as the former provides a better control for changes in the mix of sales between more and less expensive properties.
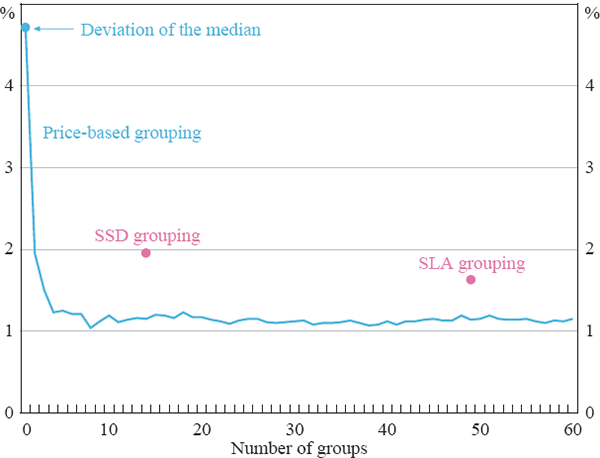
Source: Authors' analysis using data from APM
An important additional result in Figure 4 concerns the ‘granularity’ of stratification in our price-based measures. The line on the graph shows how the deviation from trend (as a RMSE) varies according to the number of strata used to calculate price growth. We see that simply dividing all transactions into two groups of about 330 suburbs produces notable gains over the median measure. There are further significant gains from splitting the sample into four groups, but thereafter the RMSE is fairly constant. This implies that one can get fairly comparable estimates of movements in Sydney house prices by dividing Sydney's 659 suburbs into anything from 4 to 60 groups: this is also confirmed by correlation analysis. Therefore, the results for Sydney that we have shown earlier in the paper are not particularly sensitive to our decision to divide suburbs into 10 groups: indeed there is a wide range of price-based stratification schemes that yield robust results.
We conjecture that the results for other cities are also not especially dependent upon our decision to group suburbs into deciles (or quintiles). We have not aimed to fit the suburbs in each capital city into an ‘optimal’ number of groups: the choice of deciles was fairly arbitrary on our part, though in cases of smaller sample sizes (houses in Canberra, and apartments in Sydney and Melbourne) we decided to instead work with quintiles to avoid small sample sizes in particular strata, especially in the incomplete real-time samples. For other applications, there will no doubt be benefits to empirically testing the optimal degree of stratification, and smaller sample sizes will presumably warrant a different number of groups, but our preliminary results here suggest that a range of strategies can yield significant benefits over simple medians.[22]
Footnotes
McCarthy and Peach (2004) find that US median prices are also volatile. Indeed, the growth rate in the nationwide median price series produced by the National Association of Realtors is 2½ times more volatile than the growth in the repeat-sales index produced by the Office of Federal Housing Enterprise Oversight. [16]
The trend is calculated using the moving-average approach described in Footnote 4. We first construct two measures of trend, one from an index version of our mix-adjusted measure and the other using the seasonally adjusted median. The measure of trend used in the comparisons in Table 4 is the average of the two measures: we do this to ensure a fair ‘horse-race’ between our measure and the seasonally adjusted measure (though the results are not sensitive to the assumptions about the calculation of the trend). [17]
We will not focus on the question of why there appears to be some correlation between the sale price of houses and the time taken for settlement, reporting and recording of transactions. However, possible explanations would be that settlement conventions tend to be longer in more expensive areas (this could be because buyers of more expensive houses are more likely to be repeat-home buyers who may want a longer settlement period so that they can finalise selling their previous dwelling), that such buyers may tend to perceive benefits from delaying reporting their transactions, or that the processing of title changes in older (more expensive) suburbs might take longer than those in newer (less expensive) suburbs. [18]
The individual sales data used contain sales recorded up to September quarter 2005. The RMSEs are calculated on data for sales from the March quarter 1996 to the June quarter 2005. [19]
We construct a measure of trend growth for each of the mix-adjusted, hedonic and repeat-sales measures (using the moving-average approach outlined in Footnote 4) and then average these three trends to obtain a proxy for underlying growth in house prices for each city. [20]
Due to some constraints in the unit record data, the results here differ somewhat from the results in Tables 4 and 5. The measures in this section are constructed using unit record data that are of a different vintage and cover a different time span (March quarter 1996 to June quarter 2005) to most of the data used in the rest of the paper. [21]
See Hansen et al (1953) and Everitt (1980) for more information on the theoretical issues in the optimal grouping of data. [22]