RDP 2006-04: Measuring Housing Price Growth – Using Stratification to Improve Median-based Measures 2. The Impact of Compositional Change on Median Price Measures
May 2006
- Download the Paper 233KB
Median or mean house price series are produced in many countries.[2] One clear advantage of median price measures is that they are very easy to calculate. They also have a straightforward interpretation: they represent the price in a ‘typical’ transaction in any given period.
However, if one is interested in inferring the price change for the overall housing stock, these measures can be distorted by compositional change. In particular, the transactions that occur in any period may not be representative of the overall housing stock. Or more importantly for estimating price changes, the composition of the sample of transactions in one period may be quite different to the composition in the next period. As a result, changes in median and mean prices may contain substantial noise from compositional change and provide poor estimates of price changes that result from changes in demand and supply conditions.
2.1 Australian Evidence
We can illustrate the problems resulting from compositional change using quarterly data for median prices of houses transacted in Sydney between March quarter 1993 and September quarter 2005. The top panel of Figure 1 shows the quarterly median price (on a log scale). The middle panel shows the quarterly change in this series along with a line for the trend quarterly growth.[3],[4] These series indicate that there was substantial growth in median prices over most of this period, but with substantial noise, which is apparent in the sometimes large divergences between the actual and trend change in the median.
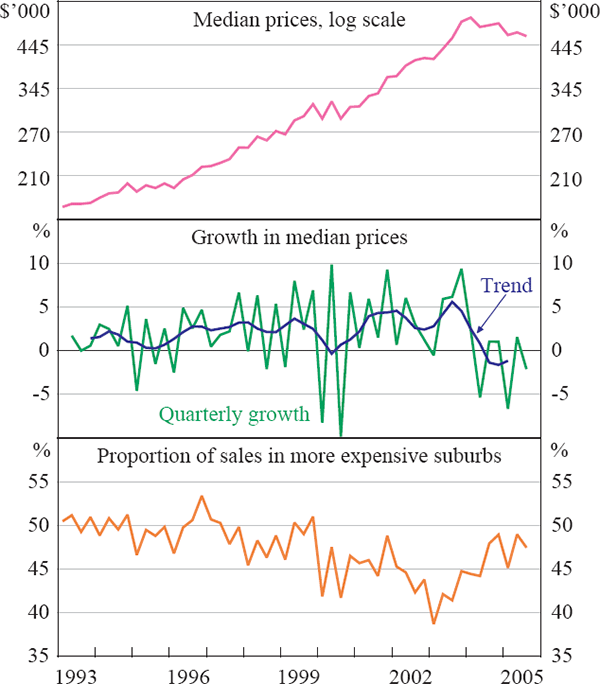
Source: Authors' analysis using data from APM
In the bottom panel of Figure 1, we introduce a measure of compositional change which may be able to explain some of the noise in the median price. To construct this variable, the 659 suburbs in Sydney were ranked according to their median transaction prices over 2000–2004, and then allocated into 10 groups (or deciles), with an approximately equal number of suburbs in each group. Decile 1 consists of the 65 suburbs with the lowest median prices, while Decile 10 consists of the 66 suburbs with the highest median prices. For each quarter, we then calculate the proportion of transactions in the more expensive suburbs (Deciles 6–10). In the case of Sydney, this proportion averages somewhat below 50 per cent because the allocation of suburbs was done to ensure a similar number of suburbs, rather than transactions, in each decile.[5] The data show that there is significant quarterly variation in the proportion of transactions in the more expensive suburbs of Sydney.[6] This leads to noise in the median measure, as measured price growth reflects both changes that result from compositional effects as well as pure price changes. An illustration of the noise in quarterly growth of the city-wide median measure is that, in most cases, quarterly growth in this series is outside the range of the middle six decile growth rates. Indeed, in nearly half of all quarters in the data sample, the quarterly changes in the city-wide median is actually outside the range of median price changes in all ten deciles (Figure 2).
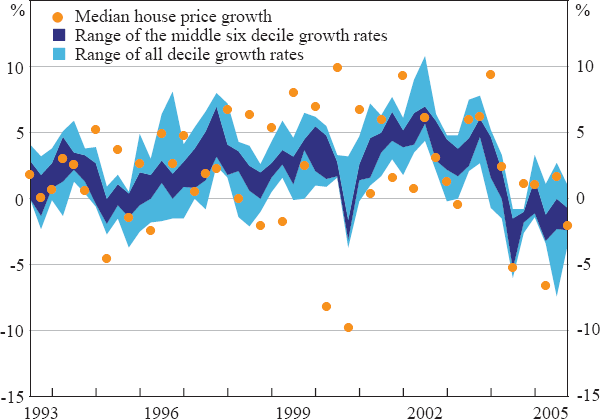
Source: Authors' analysis using data from APM
We can formally test the proposition that compositional change between higher-and lower-priced suburbs may be responsible for some of the observed noise in the change in median house prices. We regress quarterly changes in median prices on a constant and a compositional change variable, given by the quarterly change in the proportion of dwellings sold in more expensive suburbs. We estimate this equation using data from June quarter 1993 to September quarter 2005 for median house prices in the six largest cities (Sydney, Melbourne, Brisbane, Perth, Adelaide and Canberra).[7] We also estimate it for apartment prices in Sydney and Melbourne, which account for around 70 per cent of the stock of capital-city apartments. In most cases we proxy the proportion of house sales in more expensive suburbs by sales in the top five deciles. The exception is the house market in Canberra and the apartment market in Sydney and Melbourne. Given the smaller size of these markets, transactions were grouped into five groups (quintiles), and we classify the middle quintile in such a way as to have an approximately equal number of sales in the higher-and lower-priced segments.
Results are shown in Table 1. In all cases the compositional change variable takes the expected positive sign: an increase in the proportion of transactions in higher-priced suburbs leads to the change in the median price being higher.[8] For Sydney and Melbourne, the results indicate that a considerable proportion – around 60 per cent – of the quarterly variation in median house prices can be explained purely by shifts in the mix of sales between higher-and lower-priced suburbs. The effect of compositional change is notable, though less pronounced in the other markets, explaining around 20 to 40 per cent of quarterly price movements. The exception is Brisbane which appears to be much less affected by this form of compositional change. Overall, the results in Table 1 suggest fairly strongly that there may be significant gains from taking account of the effect of this simple form of compositional change on median price measures.
| Coefficient on compositional change variable |
Adjusted R2 | |
|---|---|---|
| Sydney houses | 1.09*** | 0.60 |
| Melbourne houses | 0.77*** | 0.63 |
| Brisbane houses | 0.56* | 0.05 |
| Perth houses | 0.70*** | 0.20 |
| Adelaide houses | 0.89*** | 0.26 |
| Canberra houses | 0.45*** | 0.18 |
| Sydney apartments | 0.70*** | 0.37 |
| Melbourne apartments | 0.92*** | 0.39 |
|
Notes: This table shows results from a regression to determine if the quarterly growth in median house prices over 1993:Q2–2005:Q3 is affected by changes in the composition of dwellings sold. The regression estimated is Δpt = α+βΔcomt + εt where Δpt is the quarterly change in median prices, Δcomt is the quarterly change in the proportion of transactions in more expensive suburbs, and εt is the error term. Significance at the 1, 5 and 10 per cent levels is denoted by ***, ** and *, respectively. |
||
A close look at Figure 1 suggests that part of the quarterly variation in the composition of dwellings sold may be seasonal in nature. Accordingly, we test for identifiable seasonality in the composition of sales and in the level of prices using the US Census Bureau's X12 seasonal adjustment program. In addition, we regress the quarterly change in the proportion of dwellings sold in more expensive suburbs and the quarterly change in the median price on seasonal dummies. While X12 provides a more sophisticated approach to testing for seasonality (by differentiating between trend, cyclical and seasonal influences and allowing seasonal patterns to vary over time), the adjusted R2 from the seasonal dummy variable regressions provides a straightforward way of comparing the importance of seasonality in different series.
Panel A of Table 2 contains results from testing for seasonality in the proportion of houses sold in more expensive suburbs and Panel B contains the results for median prices. Both median prices and the composition of transactions are found to be seasonal in most capital cities. Furthermore, cities where the composition of transactions is found to exhibit a seasonal pattern tend to be the ones where median prices are found to be seasonal, suggesting that at least part of the seasonality seen in median prices is the result of seasonality in the composition of sales.[9] The sign and size of the seasonal factors on the compositional change and median price also support this, with the quarters when median prices are seasonally high (typically the December quarter in most cities) tending to be the quarters when the proportion of sales in higher-priced suburbs is also seasonally high. The values for the adjusted R2 suggest that seasonal influences are particularly strong in the market for houses in the two largest capitals, explaining as much as a third (Sydney) or half (Melbourne) of the variation in quarterly price movements. Given that there is significant seasonality in most capital cities, and that the pattern of seasonality in the two largest cities is very similar, it is not surprising that there is also seasonality in average nationwide prices (which are calculated as the weighted average of prices in each capital city market using dwelling stock weights). Seasonal factors can explain nearly 40 per cent of quarterly price movements at the national level.
| Is identifiable seasonality present in X12? |
Adjusted R2 from regression of quarterly change in the dependent variable on seasonal dummy variables |
|
|---|---|---|
| Panel A: Testing for seasonality in the compositional change variable | ||
| Sydney houses | Yes | 0.60 |
| Melbourne houses | Yes | 0.83 |
| Brisbane houses | No | 0.14 |
| Perth houses | Yes | 0.29 |
| Adelaide houses | Yes | 0.47 |
| Canberra houses | No | 0.05 |
| Sydney apartments | Yes | 0.53 |
| Melbourne apartments | Yes | 0.31 |
| Panel B: Testing for seasonality in median house prices | ||
| Sydney houses | Yes | 0.33 |
| Melbourne houses | Yes | 0.50 |
| Brisbane houses | No | 0.02 |
| Perth houses | Yes | 0.14 |
| Adelaide houses | Yes | 0.26 |
| Canberra houses | No | −0.02 |
| Sydney apartments | Yes | 0.26 |
| Melbourne apartments | No | 0.09 |
| Australian housing | Yes | 0.39 |
| Panel C: Testing for seasonality in selected international median and mean price series | ||
| US | ||
| Northeast | Yes | 0.23 |
| Midwest | Yes | 0.45 |
| South | Yes | 0.55 |
| West | Yes | 0.18 |
| United States nationwide | No | −0.02 |
| Canada | ||
| Toronto | Yes | 0.29 |
| Canada nationwide | Yes | 0.11 |
| NZ | ||
| Auckland | No | 0.02 |
| Waikato/Bay of Plenty | Yes | 0.11 |
| Wellington | Yes | 0.55 |
| Canterbury/Westland | Yes | 0.09 |
| New Zealand nationwide | Yes | 0.11 |
| Note: The Australian sample covers 1993:Q1–2005:Q3; the overseas data covers varying periods (see Footnote 10). | ||
However, the relationship between changes in median prices and changes in the proportion of houses sold in more expensive suburbs is not purely due to common seasonality. For each capital-city market, we have also regressed quarterly changes in seasonally adjusted median prices on a constant and the seasonally adjusted compositional change variable. The adjusted R2s from these regressions are lower than those in Table 1. However, in nearly all cities (the exceptions are Brisbane and Adelaide) the seasonally adjusted compositional change variable can explain a notable amount of the quarterly change in the seasonally adjusted median price, with adjusted R2s ranging from between 0.10 (for Perth houses) to 0.37 (for Melbourne apartments). Therefore, there also exist significant non-seasonal shifts in the proportion of sales in more and less expensive suburbs that will be reflected in movements in median prices.
2.2 International Evidence
We have not been able to do similarly detailed tests of the impact of compositional change on median prices for other countries due to the absence of similar time series data for the share of transactions in different segments of the market. However, in Panel C of Table 2 we apply similar tests for seasonality to some readily available international housing price series. These are the median series produced by the US National Association of Realtors and by the Real Estate Institute of New Zealand (only major regions are shown) and the mean series from the Real Estate Institute of Canada.[10] The results are comparable to Australian data, with median and mean prices in nearly all regions found to be seasonal. In some cases, seasonal dummies alone are able to explain a significant proportion of the quarterly variation in prices.
We can think of no compelling reason as to why pure house price changes should be seasonal. Accordingly, the results suggest that price measures in these countries are also being significantly affected by compositional change, consistent with observations made by others (for example, McCarthy and Peach 2004, p3 and REINZ 2005). It therefore appears that the problem that we address in this paper may be a fairly general one, suggesting that the solution proposed here may also have wider relevance for house price measures published in some other countries.
Footnotes
In Australia, the price data produced by the Real Estate Institute of Australia and the Commonwealth Bank are simple unstratified medians (with no allowance for possible seasonality). In addition to the measures already mentioned, many house price measures in continental Europe also use a mean or median to measure prices, for example, measures constructed in Belgium, Denmark, Ireland, Luxembourg, Norway and Switzerland. [2]
Through the rest of the paper, all calculations involving changes in prices use the change in the log of the price series. In cases where we show these in a table, they are the log change multiplied by 100 so as to correspond approximately to percentage changes. [3]
The trend is calculated as the change in the five-quarter-centred moving average of (the log of) the median price series. The weights in the moving average are 0.125, 0.25, 0.25, 0.25, and 0.125, which should remove any seasonality from the trend. [4]
All the raw data used in this paper, including the division of data into deciles, has been provided by Australian Property Monitors (APM). The results in Sections 5.3 and 5.5 are based on unit record data provided by APM. [5]
It is interesting that there also appears to be a downward trend in this ratio over most of the sample, perhaps because the growth in the city has been in suburbs relatively far from the centre, which tend to be less expensive suburbs. This suggests that measures of median prices might understate true longer-run price growth over the entire period. We do not address this issue, but instead focus on improving estimates of short-run changes in house prices. [6]
Houses are defined to include both detached and semi-detached dwellings. [7]
We have also regressed the compositional change variable on our stratified measure of price changes, which account for compositional change. The results indicate that there is no tendency for the compositional change variable to be related to true changes in house prices, so the results in Table 1 reflect spurious compositional effects on median prices. [8]
It is beyond the scope of this paper to consider the reasons for the seasonality in the composition of sales. However, it is interesting that in each of the capital cities where sales volumes are found to be most seasonal, the seasonality comes more from variation in the sales volumes in higher-priced suburbs than in lower-priced suburbs. This would be consistent with some cities having particular ‘selling seasons’, especially in higher-priced suburbs. [9]
The series for the US, Canada and New Zealand refer to existing one-family homes, dwellings, and existing dwellings, respectively. The analysis uses data for 1975:Q2–2005:Q4 for the US, 1980:Q1–2005:Q4 for Canada and 1992:Q1–2005:Q4 for New Zealand. The US data have been converted to a quarterly series by averaging the monthly series. [10]