RDP 2006-04: Measuring Housing Price Growth – Using Stratification to Improve Median-based Measures 4. A Measure of Average Price Changes which Controls for Compositional Changes
May 2006
- Download the Paper 233KB
Based on the discussion in Sections 2 and 3, we propose a measure of changes in average housing prices that controls for one important form of compositional change. We refer to this hereafter as the change in the mix-adjusted measure.
4.1 Data and Method of Stratification
Our measure uses data for March quarter 1993 to September quarter 2005, prepared by APM. The dataset provided by APM contains virtually the entire population of housing transactions that occurred over this period.
As a starting point, transactions were grouped together by location, based on the suburb where the property is located.[13] However, because a city like Sydney has in excess of 600 suburbs, this would be too great a level of disaggregation to be practical if simplicity of calculation is one of the key considerations for a simple mix-adjusted measure. Further, it is likely that during some quarters the number of sales within a suburb may be quite small (or zero), hindering the estimation of a price movement for that suburb. Therefore an additional criterion is required to cluster together individual suburbs and hence reduce the number of strata.
For simplicity, median sale prices in each suburb over the period 2000–2004 were used to group suburbs into strata. For the house price data, suburbs in the five largest cities were grouped into deciles, each with an approximately equal number of suburbs, based on median prices over 2000–2004. For example, of the 446 suburbs in Melbourne, the first stratum for Melbourne consists of the 44 suburbs with the lowest median prices, while the tenth stratum consists of the 45 suburbs with the highest median prices. In the case of house prices for Canberra and apartment prices for Sydney and Melbourne, there are fewer transactions, so we group them into quintiles of equal number of suburbs.
There would, of course, be many other ranking periods that we could use for grouping suburbs into strata based on median prices. For example, we could use the median price of suburbs in 1992 to form strata for 1993, then the median prices for 1993 to form strata for 1994, and so on. However, in practice there is a very high degree of stability in the relative price rankings of suburbs: suburbs that tend to be relatively expensive in one period will tend to be relatively expensive 10 years later. Figure 3 illustrates this using data for Sydney, showing that the price relativities in the 2000–2004 sorting period also hold outside that period.[14] The same result holds almost without exception for all cities and for both houses and apartments. Hence, any reasonable alternative price-based strategy for ranking suburbs would result in very similar strata, and very similar estimates of price growth.
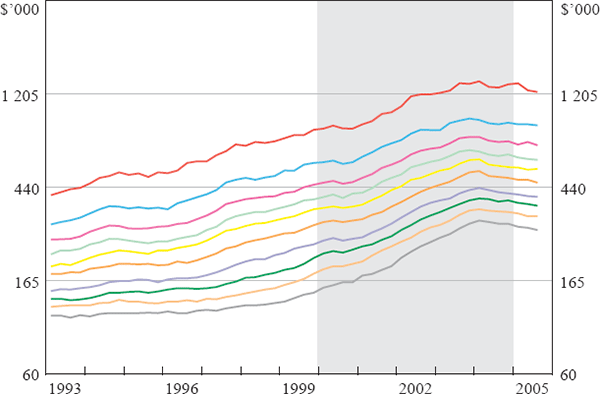
Notes: The lines represent the median price for each of the 10 deciles in Sydney. The shaded area shows the period used to sort the data.
Source: Authors' analysis using data from APM
4.2 Calculation of City-wide Quarterly Price Changes
Once suburbs were grouped into deciles (or quintiles), a median price was calculated for each strata for each quarter. The change in the median prices for each strata were then weighted together to calculate growth in city-wide prices.
There are a number of different weighting schemes that could be used to combine these ten (or five) growth rates. The simplest method would be to take an unweighted average of the changes. This is equivalent to constructing a city-wide index as the unweighted geometric average of median prices in each strata. Alternatively, we have also investigated the effect of using weights based on sales volumes over the 12-year period, and weights based on principal components (where changes in prices for any group can be thought as given by an unobservable city-wide movement plus an idiosyncratic component).[15]
However, different weighting schemes make very little difference to estimates of short-term price growth. In our sample, the different weightings yield measures of quarterly price changes which typically have a correlation of over 0.99. This reflects the fact that price changes in the different strata are typically reasonably highly correlated (see Appendix A). Nevertheless, in most cases, sales volumes and principal components imply weights for each stratum that are close to equal weights. Given that equal-weighting produces similar results to other weighting schemes and given that it is the simplest method of weighting the series, all the results shown in subsequent sections of this paper refer to the equally-weighted measure (which is labelled as the ‘mix-adjusted measure’).
Footnotes
The use of suburbs rather than postcodes allows a greater degree of disaggregation as postcodes often incorporate more than one suburb. [13]
The Spearman rank correlation between median suburb prices in Sydney in 1996 and 2004 is 0.95, which confirms that suburbs tend to maintain their relative price rankings. [14]
If the intention is to measure changes in the value of the housing stock, the most appropriate weighting would be to use suburb-level dwelling stock weights. Data limitations prevented this for the current exercise, but the results are likely to be little different to the results presented here, especially for short-term price movements. [15]