RDP 2008-04: A Small BVAR-DSGE Model for Forecasting the Australian Economy Appendix D: Impulse Responses
September 2008
D.1 Identification of the Structural Model
While it is not necessary to identify the structural VAR for the purpose of forecasting, Del Negro and Schorfheide (2004) demonstrate how it is possible to do so. This enables us to compute impulse responses that can be used to provide economic interpretation of the forecasts. Briefly, the mapping between the reduced-form and structural model is
where: Σtr is the Cholesky decomposition of Σu
(that is, ΣtrΣ′tr
= Σu, with Σtr lower triangular);
Ω is an orthonormal matrix and εt is a vector
of structural shocks. Essentially, the Cholesky decomposition allows us to
identify the structural model, but only up to a rotation (Ω). The insight
from Del Negro and Schorfheide (2004) is that we can use the DSGE to pick
Ω by equating the instantaneous effects of the structural shocks from
the DSGE and the VAR. To do this, note that for the DSGE model there exists
a matrix A0(θ) that gives this contemporaneous
effect, that is, 
. Applying a LQ transformation (akin to a
QR transformation) to A0(θ) yields
A0(θ) = LQ, where L is
a lower-triangular matrix and Q is orthonormal. Alternatively, from
the VAR, Equations (1) and (D1), 
. Consequently, we
set Ω = Q.
D.2 BVAR-DSGE Impulse Responses
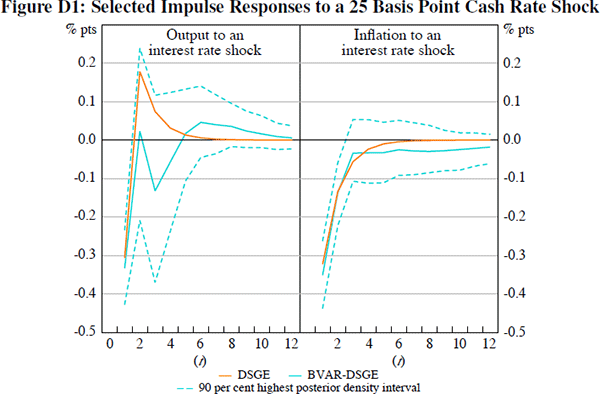
Figure D1 shows the DSGE impulse responses (orange lines) and the BVAR-DSGE impulse responses (blue lines, with the corresponding 90 per cent highest posterior density intervals) for a shock to the cash rate of 25 basis points.[22] In the BVAR-DSGE, the maximum reduction in inflation is around 0.35 percentage points, which is somewhat larger than the 0.1 percentage point reduction reported in Nimark (2007) or the 0.05 percentage point reduction found by Jääskelä and Nimark (forthcoming). We also estimate the peak impact of a 25 basis point monetary policy shock on output growth to be around 0.3 percentage points, which is larger than in Jääskelä and Nimark (0.1 percentage points). Relative to the DSGE model, the BVAR-DSGE suggests that the impact of a monetary policy shock on output growth is more prolonged.
Footnote
A 1 standard deviation shock is approximately equal to 8 basis points. [22]