RDP 2008-04: A Small BVAR-DSGE Model for Forecasting the Australian Economy 5. Forecasting Performance Comparison
September 2008
5.1 The Benchmarks
In order to examine the forecasting gain from using priors from a DSGE model, we need some benchmark models. There are several natural candidates. The first is an unrestricted (reduced-form) VAR, which makes no attempt to identify the structural shocks.[18] The second is a Bayesian reduced-form VAR with Minnesota-style priors. Minnesota BVARs historically have proven to be a useful forecasting tool (for a recent Australian example see Gerard and Nimark 2008). Briefly, a Minnesota VAR prior usually assumes that the level of each series is highly persistent, that is, they follow a unit root (possibly with drift). Consequently, the mean of the prior for the coefficient on the first own lag is one, and the mean of the priors for the coefficients on other lags are zero, and these priors are held more tightly for longer lags.[19] To make them comparable, the unrestricted and Minnesota VARs were estimated using the same variables as were observable for the BVAR-DSGE. As some of these series (such as output) are already expressed as growth rates rather than levels, the Minnesota prior was modified so as to have a mean of zero for their first own lag.[20] For simplicity we impose the same lag length of three across the models. Finally, another natural benchmark is the DSGE model itself, which we approximate by setting λ = 100,000. The forecasts from these benchmark models were constructed in the same way as those for the BVAR-DSGE.
5.2 Forecast Comparisons
To evaluate the forecasting performance of the models we construct out-of-sample forecasts and compute their RMSE. Table 4 presents the forecasting performance of the BVAR-DSGE relative to the benchmark models.
| Variable | One quarter ahead | Four quarters ahead | Eight quarters ahead |
|---|---|---|---|
| Quarterly | Year-ended | Year-ended | |
| Relative to unrestricted VAR | |||
| Output growth | 0.84 | 0.89 | 1.08 |
| Nominal cash rate | 0.80 | 0.61 | 0.79 |
| Underlying inflation | 0.84 | 1.08 | 0.99 |
| Relative to DSGE | |||
| Output growth | 0.88 | 0.94 | 1.05 |
| Nominal cash rate | 0.88 | 1.44 | 1.24 |
| Underlying inflation | 1.06 | 0.87 | 0.79 |
| Relative to Minnesota VAR | |||
| Output growth | 0.92 | 0.74 | 0.96 |
| Nominal cash rate | 0.44 | 0.89 | 1.02 |
| Underlying inflation | 1.00 | 1.13 | 0.96 |
| Note: The interest rate forecasts are for its level at all horizons. | |||
To interpret this table, note that if the entry in a particular cell is less than one, then the BVAR-DSGE outperforms the corresponding benchmark model. Focusing initially on the UVAR, this is always the case for the one-quarter-ahead forecasts. It is also true for output one year ahead, but not for inflation. Compared to the DSGE model alone, the BVAR-DSGE performs well at forecasting inflation at long horizons. The gain in forecasting performance may reflect the tendency for DSGE models to be under-parameterised. The combination of a DSGE with a VAR model increases the number of free parameters, allowing for better fitting of the data. However, the DSGE outperforms in forecasting the cash rate, apart from one quarter ahead. This was expected since when we selected the relative weighting on the DSGE model we placed more importance on the output and inflation forecasting accuracy, partly at the cost of interest rates.
Compared to the Minnesota VAR we see some moderate forecasting gains. The BVAR-DSGE forecasts more accurately both output growth at any horizon and the cash rate one year ahead. The inflation forecasts of the BVAR-DSGE are competitive. These results suggest that the theoretical information in the DSGE prior is a useful complement to the purely statistical Minnesota prior.
Overall, the results show that the BVAR-DSGE is competitive at forecasting inflation and output. Table 5 presents the absolute forecasting performance of the BVAR-DSGE model.
| Variable | One quarter ahead | Four quarters ahead | Eight quarters ahead |
|---|---|---|---|
| Quarterly | Year-ended | Year-ended | |
| Output growth | 0.33 | 0.61 | 0.79 |
| Nominal cash rate | 0.20 | 0.58 | 0.62 |
| Underlying inflation | 0.16 | 0.34 | 0.32 |
| Change in nominal TWI | 3.07 | 8.79 | 8.81 |
| Change in terms of trade | 1.34 | 4.68 | 7.01 |
| Note: The interest rate forecasts are for its level at all horizons. | |||
The RMSEs of the three key variables – output growth, underlying inflation and the cash rate – are noticeably lower than those for the exchange rate and terms of trade growth, which is unsurprising given the volatility in the latter series, as mentioned previously.
Footnotes
The UVAR was estimated in EViews 6.0. [18]
More precisely, the standard deviation of the prior on coefficient Φpjk (recall p denotes the lag length) is
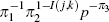 ,
where I(j,k) is an indicator function that equals
1 if j = k, and 0 otherwise. π1
is the overall tightness of the prior, which we set at 0.2. π2
enables the prior to be tighter on lags of other variables, however, as we use an
Inverted-Wishart Normal prior and Gibbs sampling we impose π1
= π2 (see Kadiyala and Karlsson 1997). Finally, π3
> 0 imposes a tighter prior on longer lags, and we set this to 0.5 (this is known
as harmonic decay). Estimation was conducted in WinRATS 7.0 by Estima, using
code by Tom Doan available on the Estima
website (<www.estima.com>). One thousand observations were
discarded as burn-in.
[19]
,
where I(j,k) is an indicator function that equals
1 if j = k, and 0 otherwise. π1
is the overall tightness of the prior, which we set at 0.2. π2
enables the prior to be tighter on lags of other variables, however, as we use an
Inverted-Wishart Normal prior and Gibbs sampling we impose π1
= π2 (see Kadiyala and Karlsson 1997). Finally, π3
> 0 imposes a tighter prior on longer lags, and we set this to 0.5 (this is known
as harmonic decay). Estimation was conducted in WinRATS 7.0 by Estima, using
code by Tom Doan available on the Estima
website (<www.estima.com>). One thousand observations were
discarded as burn-in.
[19]
By using the same variables we may, to some extent, make the benchmark models ‘straw men’; for example, if one was independently constructing a Minnesota BVAR then possibly a larger or different set of variables could be used. [20]