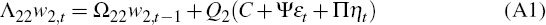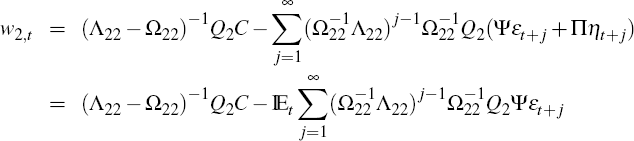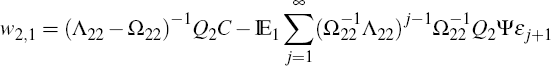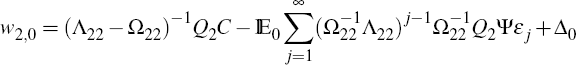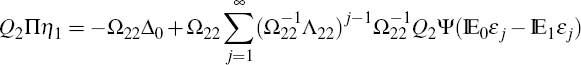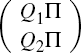RDP 2008-10: Solving Linear Rational Expectations Models with Predictable Structural Changes Appendix A: Proof of Propositions 1 and 2

Proof of Proposition 1

Proof

Sufficiency: If rank(Q₂π) = m, then the columns of Q₂π span 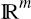. This means that for arbitrary initial conditions and for any fundamental shock, expectation revisions can keep the system on its SSP.

Necessity: w_2,t must satisfy

To be on the SSP, w_2,t must also satisfy

and more specifically

Now suppose the initial condition of the system, y₀, is arbitrary, so that the economy may not necessarily be on the SSP. We can then write 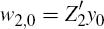as the sum of a component that is on the SSP and some deviation from the SSP value

where 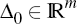We can look at Equation (A1) from the perspective of period 1 to show that in order for equality to hold (that is, for the system to be on the SSP in period 1), the following condition must be satisfied

Since Δ₀ is arbitrary, we require the columns of Q₂π to span 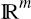. Since Q₂π is m × k, this is equivalent to requiring rank(Q₂π) = m.

Proof of Proposition 2

Proof

Sufficiency: Suppose that rank(Q₂π) = k, then the rows of Q₂π span . Therefore, rowspace(Q₁π) ⊆ rowspace(Q₂π) since the rows of Q₁π necessarily span some subspace of .

Necessity: Suppose that the solution is unique. This means that rowspace(Q₁π) ⊆ rowspace(Q₂π).

We know that Q is a full rank n × n matrix. Post-multiplying by π extracts the last k columns of Q. Since Q was full rank, Qπ must have rank k. If the solution is unique, then this means that the rank of

should have the same rank as that of Q₂π. But since the matrix above is exactly Qπ, this implies that the rank of Q₂π is k.