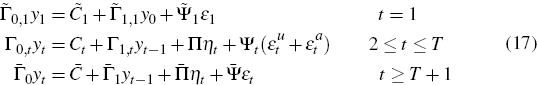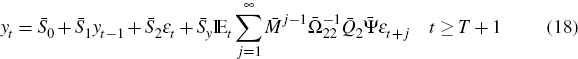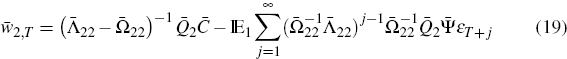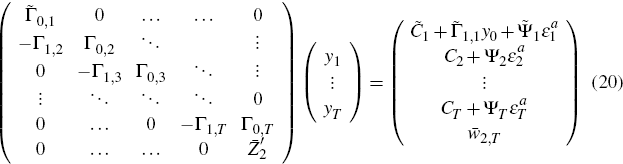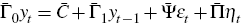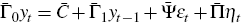RDP 2008-10: Solving Linear Rational Expectations Models with Predictable Structural Changes 3. The Rational Expectations Solution with Predictable Structural Changes

In this section, we propose a method to solve LRE models when there is a sequence of anticipated events. These events encompass anticipated changes to the structural parameters of the model or anticipated additive shocks. We assume that within a finite period of time, the structural parameters of the model converge and no further shocks are anticipated.

At the beginning of period 1, agents know the previous state of the economy, y₀, the fundamental shock ε₁, they anticipate a sequence of shocks 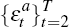, and know how the structural parameters will vary in the future, 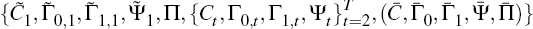That is, the system evolves as follows

where 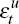represents unanticipated shocks to the system and 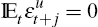for j ≥ 1. The reason for identifying these shocks separately is because as time unfolds, actual shocks may be different from what were originally expected so that in any period, we can decompose a shock as the sum of its anticipated and unanticipated components 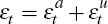. We could alternatively include 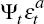as part of C_t, but we identify the shocks separately to illustrate how the solution for predictable structural variations encompasses anticipated additive shocks as a special case.

Assuming a unique solution exists for t ≥ T + 1, the reduced form of the system can be computed as discussed in the previous section as follows

where 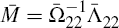This solution helps us compute y_t for t ≥ T + 1, given y_T. The aim of this section is to solve for y₁ ,y₂,...,y_T given all anticipated structural variations and additive shocks.

Since y_t is (n₁ + n₂ + k) × 1, we require at least T × (n₁ + n₂ + k) independent equations to obtain a unique solution for 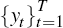. Notice that:

• for each period, we have (n₁ + n₂) equations as defined by Equation (1). This gives us T × (n₁ + n₂) equations;
• for t = 2,...,T, rational expectations requires η_t = 0. From the perspective of period t = 1, there should be no forecast errors or revisions to expectations. This gives us (T − 1) × k equations; and
• if a stable solution exists for t = T + 1 onwards, then 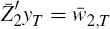, where 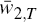is given by

Equation (19) gives 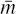equations where 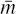represents the number of explosive eigenvalues of the final (bar) system. 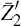is from the QZ decomposition of 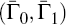and therefore has 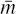independent rows. The last condition is effectively a terminal condition that guarantees that the system is on its SSP for t ≥ T + 1. In total, we get 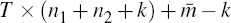equations that can be summarised as follows

The condition that η₂,...,η_T = 0 implies that πη_t = 0 for t = 2,...,T. Also notice that the structure of 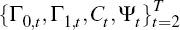guarantees that 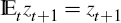since the last k rows of C_t and Ψ_t are zero for all t.

Solving for y₁,...,y_T involves solving a linear system of the form Ay = b, where 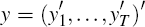and A stands for the matrix on the left while b stands for the vector on the right-hand side of Equation (20). Propositions 1 and 2 imply that for the final (bar) system to have a unique solution, 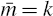; in this case, Equation (20) has as many equations as there are unknowns. However, if the final (bar) system has many solutions, 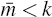, then Equation (20) forms a system with less equations than unknowns, in which case, if there is a solution, there are infinitely many. Obviously, the existence of a solution to the structurally invariant final system is a necessary condition for Equation (20) to have a solution. We summarise these two observations with the following propositions.

Proposition 3. Existence of a solution to the final (bar) system

is necessary for the existence of a solution to Equation (20).

Proposition 4. Uniqueness of a solution to the final (bar) system

is necessary for the uniqueness of a solution to Equation (20).

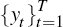The propositions above state necessary but not sufficient conditions for the existence and uniqueness of a solution for . The existence and uniqueness of a solution for 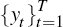ultimately depend on the properties of the matrix A. We have shown that if a unique solution exists for the final structure, A is a square matrix. Next, we argue that A will generally be a full-rank matrix for the following reasons:

• The rank of the matrix (−Γ_1t Γ_0,t) is n for t = 2,...,T. If not, there are linearly dependent and possibly inconsistent equations; a sort of ill-specified problem.
• The block bi-diagonal structure of the matrix A implies that none of the rows associated with period t can be obtained as a linear combination of rows associated with non-adjacent periods. If this is the case, this implies that for some period, the rank of the matrix (−Γ_1t Γ_0,t) will be less than n for some t, violating the preceding point.
• For a well-defined system, the rows of 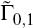will be linearly independent. So the first n₁ + n₂ rows of A will be linearly independent.
• The rows of 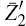are linearly independent because 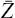is unitary. So the last k rows of A will be linearly independent.
• In general, no row, for a given period, can be expressed as a linear combination of the rows associated with that period and from an adjacent period. This would mean that Γ_1,t and Γ_{0,t+ 1} are rank deficient. Even if this were the case, suppose for non-zero vectors, w and v, wΓ_1,t = vΓ_0,t+1 = 0, then we would also require that wΓ_0,t − vΓ_1,t+1 = 0 if there were a linear dependency in rows associated with periods t and t + 1. Although this is possible, we argue that this seems unlikely.
• The last k rows are linearly independent of the first nT − k rows. Clearly, the last k rows are linearly independent of the rows associated with periods 1,...,T − 1, for the same reasons we discussed earlier for non-adjacent periods. But, in general, the last k rows of A are linearly independent of the preceding n rows. If a linear combination of the rows of 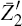reproduce a row of Γ_0,T, that same linear combination of zero vectors must reproduce the corresponding row of −Γ_1,T, which may not necessarily be zero. 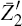is typically unrelated to Γ_0,T because it comes from the QZ decomposition of 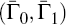. But even if 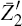came from the QZ decomposition of (Γ_0,T, Γ_1,T), it relates to Γ_0,T in a non-linear fashion.

The arguments above imply that the matrix A will be invertible, in which case, the solution for 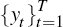will be unique. However, it is possible that A is not invertible under some perverse parameter variations. Under such circumstances, the existence of solution requires b to be contained in the column space of the matrix A; but this is not a guarantee that any such solution will be unique. The invertibility of A obviously guarantees that there is a unique solution.

This suggests that the way in which parameters vary can determine whether a unique solution exists or not. For instance, should a policy-maker decide to change the parameters of the policy rule over a set length of time, it might matter how this policy change is implemented over time for a unique equilibrium path to exist.

So we conclude that, in general, the existence and uniqueness of a solution for 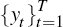will hinge on the existence and uniqueness of a solution to the final structure.

The solution method we propose has a number of advantages: it is simple to implement as it only requires solving a matrix inversion problem; even in the absence of structural changes, it enables us to forecast over finite horizons without resorting to loops; and it can be used recursively to produce stochastic simulations in the face of fully predictable structural variations.