RDP 2009-02: Competition Between Payment Systems Appendix B: Platforms' Pricing Incentives
April 2009
In this Appendix we use the geometric frameworks developed in Section 3 to briefly examine, at a theoretical level, the incentives facing platforms in their pricing decisions. Further details of the analysis sketched here are provided in Gardner and Stone (2009b), while actual simulation analysis of these incentives and their implications is carried out in Gardner and Stone (2009a). Note that, for the purposes of the discussion below, we assume for simplicity that no non-uniqueness issues arise, along the lines described in Section 4, for any of the fee settings under consideration.
B.1 The Effects of an Increase in a Platform's Consumer Fee
Consider the case of a platform contemplating raising its flat fee to consumers.[35] Before doing so it must take into account that, even with unchanged merchant acceptance, this might cause some consumers to switch to the rival platform, and cause others to abandon cards altogether in favour of cash. These would be the direct effects of such a fee increase.
However, they are not the only effects such a change would have on the platform's position in the market. The reduction in consumers subscribing would, in turn, reduce the number of merchants wishing to sign up to the platform. This would then not only further affect the platform's expected profit but also generate third-round effects back on the consumer side (by further reducing the incentive for consumers to hold the platform's card), and so on.
The frameworks developed in Section 3 give a way of tracing
through these effects, conveniently broken into direct, second-, third- and
later-round impacts as just
described.[36]
For the case of a marginal increase in platform i's flat fee
to consumers, with the other platform's fees held fixed, the first few
rounds of these impacts are illustrated in Figures B1 to B3. In these figures
we assume that the fee change is from a starting equilibrium where  , so that the consumer
side of the market may initially be represented as in Figure 3.
, so that the consumer
side of the market may initially be represented as in Figure 3.
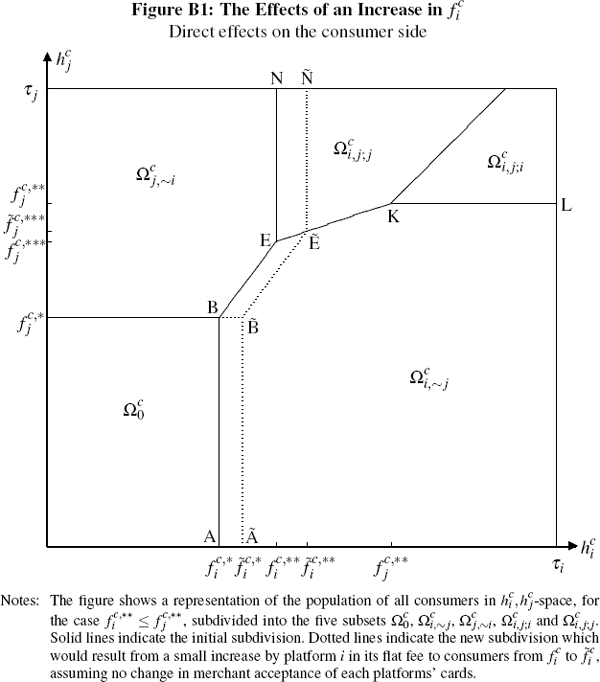
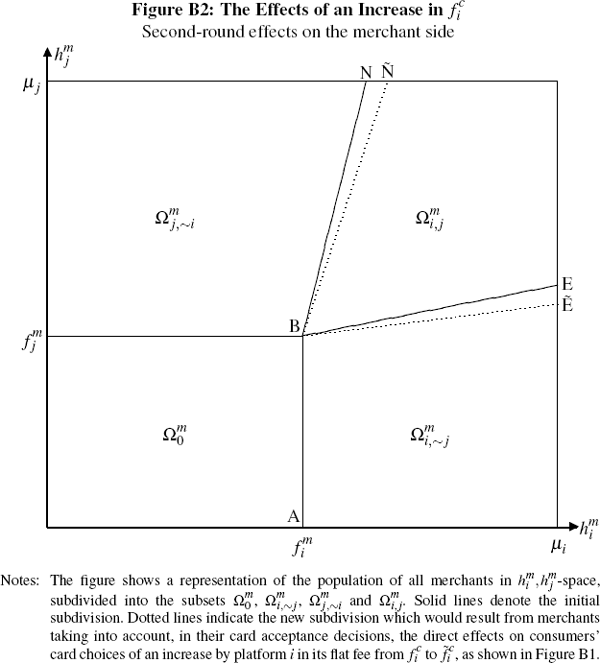
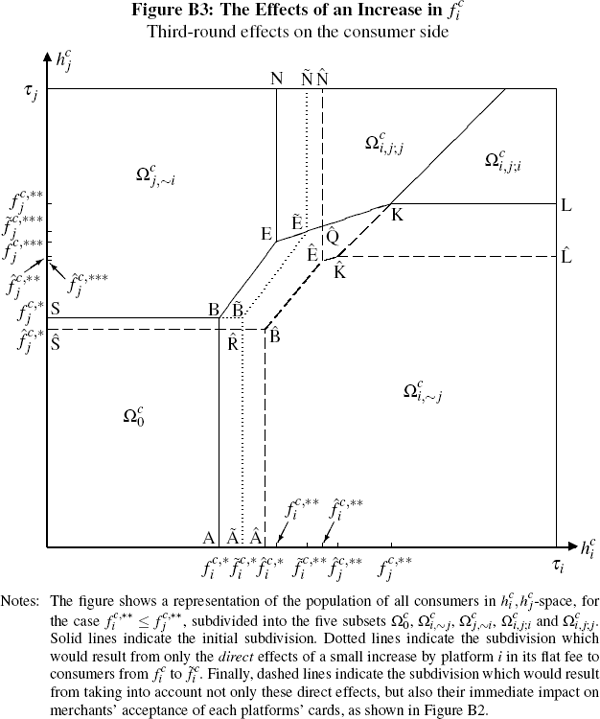
Clearly, we could also, in principle, continue such diagrammatic analysis to consider fourth-round effects on merchants from the third-round changes in consumers' card holding decisions, fifth-round effects on consumers from these fourth-round impacts, and so on. However, rather than doing so we content ourselves with two observations.
The first is that we would expect any fourth- (or sixth-, eighth-, etc) round effects to resemble, in general terms, the second-round effects discussed above – being driven as they would be by shifts in consumers' card holding choices. Similarly, we would expect any fifth-, seventh-, etc round effects to resemble the third-round effects discussed above (rather than the direct effects), being the result not directly of a price change but indirectly of changes in merchants' card acceptance patterns.
The second observation is that, while not guaranteed, one might hope that iterative breakdowns like this would see the bulk of any impacts concentrated in the first few rounds, with later-round effects becoming less and less significant. Happily, numerical checks for a range of scenarios suggest that this is typically so – at least where, as assumed here, no issues of non-uniqueness arise. Hence, examining up to third-round effects generally seems to be sufficient, in such circumstances, to understand how a given fee change by one platform would be expected, ceteris paribus, to affect the card holding and acceptance decisions of both consumers and merchants.
B.2 The Impact on a Platform's Profits and Incentives
For any starting configuration of fees, the sort of analysis in Section B.1 would allow each platform to assess the impact on its equilibrium consumer and merchant base of a shift in its pricing – at least for unchanged fees on the rival platform. This would, in turn, allow each platform to determine the effects on its (and its competitor's) profits of such a shift, and so weigh its incentives to proceed.[37]
These latter effects are traced through in detail in Gardner and Stone (2009b), where a discussion is also provided of how the profit impacts and incentives would change in the event that the two platforms were not rivals, but rather were operated by a monopoly provider of card payment services. Without repeating that discussion here, an illustration of these effects is provided by Table B1, which summarises these profit impacts for the case of the third-round effects of a small increase in platform i's flat fee to consumers (as depicted in Figure B3).
| Change in card choice | Consumers affected |
Impact on Πi in duopoly | Impact on monopoly profit (Πi+Πj) |
|---|---|---|---|
| A. Impact on net subscription revenue | |||
| Hold i only → No cards | Region  |
− | − |
| Hold i only → Hold j only | Region  |
− | ? |
| Hold i only → Hold i and j | |||
| Prefer to use i | Region  |
* | + |
| Prefer to use j | Region  |
* | + |
| Hold i and j but prefer j | |||
| → Hold j only | Region  |
− | − |
| No cards → Hold j only | Region  |
* | + |
| B. Impact on net transaction revenue | |||
| Hold i only → No cards | Region  |
− | − |
| Hold i only → Hold j only | Region  |
− | ? |
| Hold i only → Hold i and j | |||
| Prefer to use i | Region  |
* | + |
| Prefer to use j | Region  |
− | ? |
| Hold i and j but prefer j | |||
| → Hold j only | Region  |
− | − |
| No cards → Hold j only | Region  |
* | + |
Notes: For each category of change in consumers' card holding choices,
the table separates the impacts of such changes into two parts: Part A
shows the impact on profit from resultant changes in net subscription
revenue; Part B shows the impact on profit from resultant changes in transaction
volumes. Results shown are for the scenario discussed in Section B.1,
where it was assumed that  initially. Results also assume that
prior to the fee increase initially. Results also assume that
prior to the fee increase  and and  , as discussed
in Footnote 38. , as discussed
in Footnote 38. |
|||
Six distinct effects on consumers' card holding behaviour may be identified in Figure B3 and, for each category, its profit impact may be separated into two parts: that from resultant changes in net subscription revenue, shown in Part A of Table B1; and that from resultant changes in transaction volumes, shown in Part B.[38]
As is evident from the table, for just two of the six categories of changes are the profit impacts identical in the duopoly and monopoly cases. The first is those consumers who would switch from holding only card i to holding no cards; and the second is those consumers who multi-home, and who prefer to use card j, who would switch to single-homing on platform j.
For all other categories the profit impacts would differ between the two cases – being always, in aggregate, less adverse for the monopolist. For example, consider the category of consumers who would switch from holding just card i to holding both cards, but with a preference to use card j. For this category, the impact on platform i's profit in the duopoly setting would be nil in terms of net subscription revenue, but clearly negative in terms of net transaction revenue (since these consumers would now switch all their transactions at those merchants who accept both cards from card i to card j). By contrast, for a monopoly operator of both platforms, the impact on net subscription revenue would be clearly positive – from the additional subscriptions on platform j – while the effect on net transaction revenue would be ambiguous rather then definitely negative.[39]
Footnotes
The corresponding analysis of the alternative case of a merchant fee increase proceeds similarly. [35]
These do not, of course, literally represent first-round, second-round and so forth effects in a dynamic sense. Rather, they represent a useful way of disaggregating the overall shift between pre- and post-change equilibria into manageable components. [36]
A further – and quite separate – complication for a platform contemplating altering its fees is, of course, the issue of how the other platform might respond to any such price change. [37]
In discussing these impacts we assume that  and
and  ,
or in other words that neither platform is initially subsidising subscriptions
or transactions (even though either possibility could conceivably be a profitable
strategy). This is done for simplicity, to rule out the possibility that
a loss of subscriptions or transactions by a platform could, at least in
its immediate impact, be profit increasing.
[38]
,
or in other words that neither platform is initially subsidising subscriptions
or transactions (even though either possibility could conceivably be a profitable
strategy). This is done for simplicity, to rule out the possibility that
a loss of subscriptions or transactions by a platform could, at least in
its immediate impact, be profit increasing.
[38]
Specifically, in the monopoly case each transaction switched from platform i to platform j would entail a loss in net transaction
revenue of  , as in the duopoly case, but also an offsetting
gain of
, as in the duopoly case, but also an offsetting
gain of  . Hence, provided
. Hence, provided  as we are assuming
here, the impact from these switched transactions would be unequivocally
less bad for a monopolist than for the operator of platform i in
a duopoly. Indeed, it might even be positive, in the event that platform
j's profit margin
on transactions,
as we are assuming
here, the impact from these switched transactions would be unequivocally
less bad for a monopolist than for the operator of platform i in
a duopoly. Indeed, it might even be positive, in the event that platform
j's profit margin
on transactions,  , were greater than that of platform i.
[39]
, were greater than that of platform i.
[39]