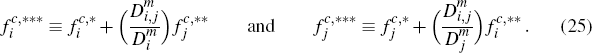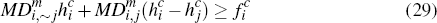RDP 2009-02: Competition Between Payment Systems 3. Understanding Merchants' and Consumers' Card Choices

Having described the general model, the next step is to try to understand what fractions of merchants and consumers will choose to sign up to none, one or both platforms, and what factors will influence these proportions. In Section 3.1 we first describe a geometric framework for thinking about merchants' card acceptance decisions, and for understanding how these decisions will be affected by platforms' pricing strategies. The more complex geometric framework for understanding the analogous decisions on the consumer side is then set out in Section 3.2.^[13] Details of the derivations of the geometric frameworks described in Sections 3.1 and 3.2 are provided in Appendix A. Finally, in Section 3.3 we show how these frameworks simplify to the versions derived and analysed in Chakravorti and Roson (2006), for the special case considered there.

3.1 Merchants' Card Acceptance Decisions

Each merchant has some draw of per-transaction benefits 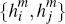for accepting a payment on platform i or j. It is possible therefore to represent each merchant as a point in 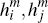-space, with the population of all merchants, Ω^m, then being distributed across the rectangle bounded by the points (0, 0), (μ_i, 0), (0, μ_j) and (μ_i, μ_j).^[14] Recall here that μ_i and μ_j denote the maximum per-transaction benefits which any merchant will receive from processing a payment on network i or j respectively.

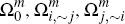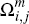Using Equations (21) to (24), it is then possible to subdivide this rectangle into four mutually exclusive regions, corresponding to the subsets and (see Appendix A for details). Doing so yields that Ω^m may be conveniently represented geometrically as shown in Figure 1.^[15]

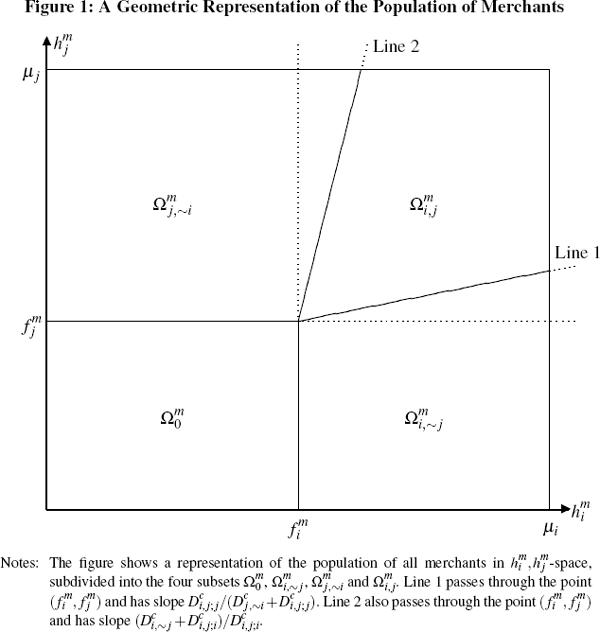
The fact that Line 1 of Figure 1 may be non-horizontal reflects that there may be some merchants who will choose not to accept platform j's cards, despite the per-transaction benefit they receive from taking a payment on platform j, 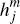, exceeding the per-transaction charge they would face for doing so. This is the phenomenon known as ‘steering’ – discussed, for example, in Rochet and Tirole (2003).^[16]

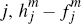For these merchants, although the net benefit they would receive from processing a payment on platform , is positive, the net benefit they would receive from processing a payment on platform 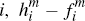, is greater again. If the difference between these net benefits is sufficiently large then, provided enough consumers who hold card j also hold card i, it may be worthwhile not to accept platform j's cards. This would see some payments shift to cash (namely, those by consumers in 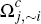), at some loss to the merchant. However, it would also steer those consumers holding both cards to pay using the cards of the merchant's preferred platform, platform i – generating a gain sufficient, for some merchants, to justify declining the cards of platform j.

3.2 Consumers' Card Choices

Turning to the consumer side, each consumer also has some draw of per-transaction benefits 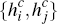for making a payment on platform i or j. Hence, we may also represent the population of all consumers, Ω^c, as being distributed across a rectangle – this time in -space, bounded by the points (0, 0), (τ_i, 0), (0, τ_j) and (τ_i, τ_j).^[17]

Using Equations (15) to (19), this rectangle can be subdivided into mutually exclusive regions – now corresponding to the subsets 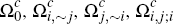and (see Appendix A for the details). Doing so yields that the population of all consumers may be represented geometrically in -space as shown in Figures 2 and 3. The added twist here, unlike on the merchant side, is that the breakdown of Ω^c turns out to differ depending on whether or not 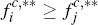. Hence, our representation of Ω^c consists of two separate diagrams, with Figure 2 depicting the situation if and Figure 3 the situation if the reverse inequality holds. 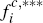Note also that, in these figures, the further notation and 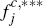is used to denote the quantities

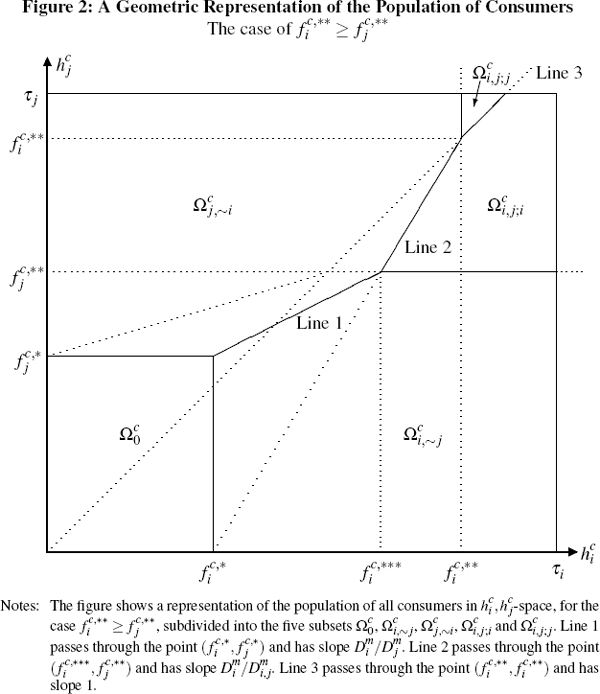
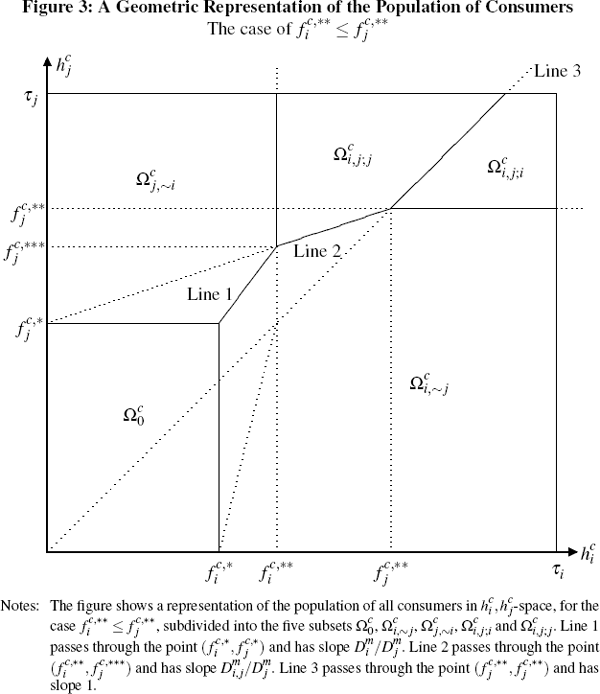
Regarding the intuition for the subdivisions shown in Figures 2 and 3, the boundaries of the region 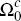are straightforward, given the definitions of the quantities 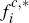and 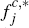(see Section 2.3). For consumers in this region, the fixed cost of holding either card exceeds the total benefit they would accrue from that card, even if they used it at every merchant that would accept it. Then Line 1, which passes through the point and has slope , simply represents the boundary between those consumers not in 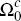who would opt to hold card i, if they could hold only one platform's card, and those who would opt to hold card j.

More interesting are the structures of the Regions and , representing consumers who choose to hold both platforms' cards. Focusing without loss of generality on the Region in Figure 2, this consists of those consumers for whom the following three inequalities all hold:

and

The intuition underlying Inequality (26) is obvious. Since consumers face no per-transaction fees, this simply represents the division between those consumers who, if they hold both cards, would prefer to use card i, and those who would prefer to use card j.

The interpretation of Inequality (27) is also straightforward. Recall that, by definition, 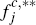is the (relatively high) effective per-transaction price that a consumer who holds both cards, but who would prefer to use card i over card j, faces for card j transactions. Hence, Inequality (27) is simply capturing that a consumer who would prefer to use card i over card j will only wish to hold both cards, rather than just card i, if the per-transaction benefit they would receive from using card j exceeds this price.

The interpretation of Inequality (28), however, is more interesting. This condition captures that, even for a consumer who would prefer to use card i over card j, it may be that he or she would still choose to sign up to platform j ahead of platform i (if, say, far more merchants will accept platform j's cards than platform i's). Hence, to wish to hold both platforms' cards, it is also necessary that the additional utility for such a consumer from signing up to platform i, if already holding platform j's card, should exceed the cost of doing so; otherwise such a consumer would be better off holding only the card of platform j. This translates directly to the requirement that

where: the first term on the left-hand side equates to the extra utility a consumer would obtain from being able to pay by card, rather than by cash, at those merchants which accept card i but not card j; and the second term corresponds to the incremental additional utility that a consumer with 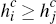would gain from being able to switch his or her card payments from platform j to platform i, at those merchants which accept both cards. This condition is then easily confirmed to be equivalent to Inequality (28) above.^[18]

A further complication on the consumer side

Finally, the need to allow for two possible cases rather than one is, unfortunately, not the only added complication with the geometric framework described above for the consumer side, relative to the merchant side. A further one relates to the magnitudes of τ_i and τ_j.

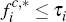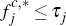As on the merchant side, we may assume without loss of generality that and . This reflects that, if either platform were to set its fees so that one or other of these inequalities failed, then that platform would attract no consumers, and hence would make no profit.

However, although for simplicity we have also drawn Figures 2 and 3 with 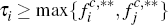and 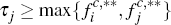, there is nothing which ensures that profit-maximising platforms will necessarily set their fees so that this will be so. Hence, for example, Figure 2 ought really to allow for the possibility that ; and also independently for the possibility that 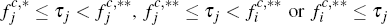(and similarly for Figure 3). Figures 2 and 3 really, therefore, each break into nine sub-cases, of which only those corresponding to the situations where τ_i and τ_j each exceed max have been shown.

These additional possibilities do not fundamentally alter the structure of Figures 2 and 3, since they essentially just alter where the lines 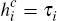and 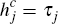sit in relation to the other parts of each diagram. However, they do significantly complicate the task of writing down equations for the fractions 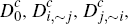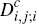and – even in the special case where consumers' per-transaction benefits are drawn from uniform and independent distributions.^[19]

3.3 The Case of the Chakravorti and Roson Model

As noted in Section 1, our model is a generalisation of that introduced by Chakravorti and Roson (2006). In their model, the restriction is imposed that consumers may only subscribe to at most one card platform. With this restriction, the geometric frameworks just derived turn out to simplify dramatically.

Considering first the merchant side, in the event that it is easily checked that Lines 1 and 2 in Figure 1 become (respectively) horizontal and vertical. Hence, Figure 1 simplifies to the situation where a merchant will choose to accept the cards of platform i if and only if , and (independently) will accept those of platform j if and only if 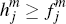. This is consistent with the fact that, when consumers hold the card of at most one platform, merchants have no scope to ‘steer’ consumers in their choice of payment card at the moment of sale, in the manner discussed in Section 3.1.

Similarly, on the consumer side, when consumers are prohibited by fiat from holding the cards of more than one platform then the subsets 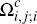and must vanish. Hence, Figures 2 and 3 reduce to the single, far simpler representation given by Figure 4 below.^[20] Note that this dramatic simplification already hints at how far-reaching the consequences can be, for the modelling of competition between payment systems, of a ‘no multi-homing’ assumption on either side of the market. This is a point to which we return in greater detail in the sequel to this paper (see Section 2.2 and Appendix B of Gardner and Stone 2009a).

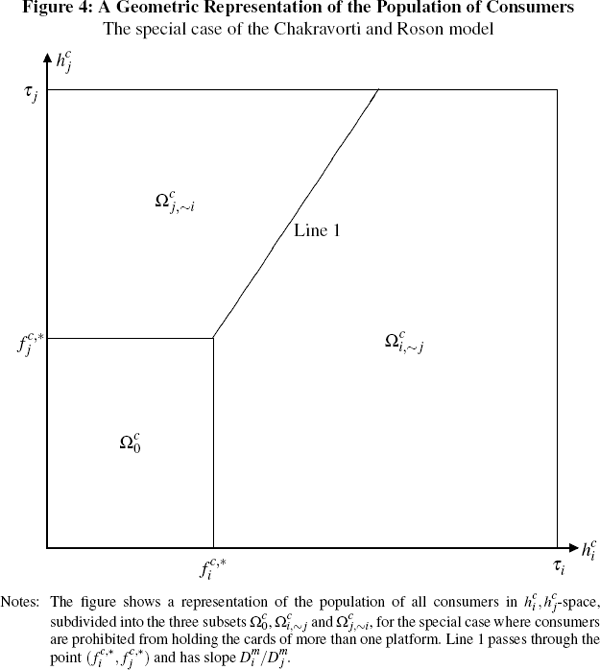
Finally, one further observation is in order regarding our ECR model and the CR model. This is that both may actually be viewed as representing special cases of a still more general model of payment system competition, obtained by incorporating an additional parameter, κ, into our ECR model. This parameter represents the disutility to a consumer from holding more than one card – say, due to the cluttering of their wallet, or the hassle of having to check two periodic transaction statements rather than one. Formally, its incorporation is accomplished simply by subtracting κ from the right-hand sides of both Equations (18) and (19) in Section 2.4 (the effects of which would, of course, then flow through to alter the frameworks set out in Section 3.2).

For this more general model, our ECR model would correspond to the special case κ = 0, while the CR model would correspond to any κ value greater than some threshold, 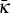, sufficient to deter even the most enthusiastic of consumers from holding more than one platform's card. While we do not pursue this idea further here, we do take it up in a different but closely related context in the sequel to this paper (see Section 5 of Gardner and Stone 2009a).

Footnotes

Having established frameworks for understanding agents' behaviour in aggregate on both the merchant and consumer sides, these frameworks are then used in Appendix B to discuss, from a theoretical perspective, the incentives facing platforms in their pricing choices. [13]

In the event that merchants' draws of per-transaction benefits are from uniform and independent distributions then the population of merchants will (on average) be evenly distributed across this rectangle, with concentration M/μ_iμ_j. [14]

Without loss of generality, Figure 1 has been drawn with 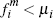and . This reflects that if either platform were to set its per-transaction fees above these levels it would attract no merchants to accept its cards and so would make no profit. [15]

The fact that Line 2 may also be non-vertical reflects corresponding steering of consumers by some merchants from platform i to platform j. Note that here we use the term ‘steering’ in the sense in which it is generally used in the theoretical literature on payment systems; that is, the refusal by a merchant to accept a platform's card, so as to force those consumers who multi-home to use a different card preferred by the merchant. This is in contrast to the colloquial sense in which the term is sometimes used, of a merchant trying to influence consumers' choices through milder means such as signs or verbal suggestions about preferred payment options. [16]

Recall here that τ_i and τ_j represent the maximum per-transaction benefits which any consumer will receive from making a payment on network i or j respectively, as set out in Section 2.4. Also, as on the merchant side, in the event that consumers' draws of per-transaction benefits, and , are from uniform and independent distributions then the population of all consumers will (on average) be evenly distributed across this rectangle, with concentration C/τ_iτ_j. [17]

An alternative derivation of Inequality (28), working directly from the utility formulae given by Equations (15) to (19), is provided in Appendix A. [18]

Of course, as on the merchant side, for the general situation of non-uniform and/or correlated distributions these equations will be even more complex, with each possible case involving the double integral over the relevant area of an appropriate (non-constant) density function. 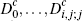For the special case where consumers' and merchants' per-transaction benefits are drawn from uniform and independent distributions, details of the equations for the quantities and are provided in a separate technical annex: see Gardner and Stone (2009b), available on request. [19]

Figure 4 is the exact analogue of Figure 1 in Chakravorti and Roson (2006), except that everything in Figure 4 is shown in per-transaction terms. By contrast, in Figure 1 of Chakravorti and Roson consumers are represented in terms of their aggregate net potential benefits (summed across all their transactions) from using the cards of platform i or platform j. [20]