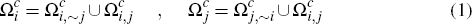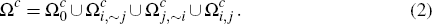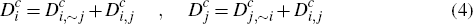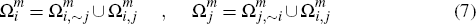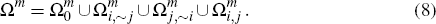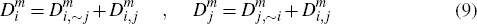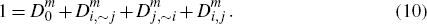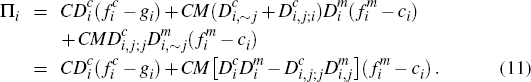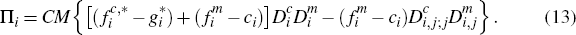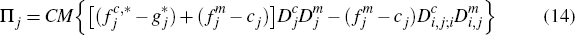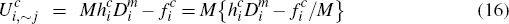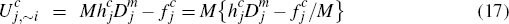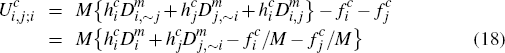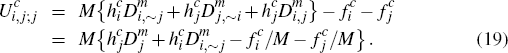RDP 2009-02: Competition Between Payment Systems 2. A Model of Competing Payment Systems
April 2009
In this section we set out the details of our ECR model of two competing payment systems. To fix ideas, and to simplify the exposition, we take these to be card payment networks. However, there is nothing inherently special about cards. Hence, the analysis which follows applies just as well in principle to non-card payment systems.
2.1 The General Model
The model contains three types of agents: a set of C consumers, denoted Ωc, a set of M merchants, denoted Ωm, and the operators of two card payment platforms, i and j. The platforms offer card payment services to consumers and merchants, in competition with the baseline payment option of cash. We focus primarily on the case where the two platforms are rivals. However, for comparison purposes, we also consider the case where both platforms are operated by a monopoly provider of card payment services.
Every consumer is assumed to make precisely one transaction with each merchant, using either cash or one of the platforms' cards. By fixing the number of transactions at each merchant, independent of the pricing decisions of the platforms, this assumption is consistent with the ‘derived demand’ aspect of payments discussed earlier. However, as noted, it also explicitly rules out ‘business stealing’ considerations from the model (see Footnote 3).
For a transaction to be made using a particular payment type, two conditions must be satisfied. First, both the consumer and merchant must have access to that instrument; for example, for a transaction to occur on platform i the consumer must hold a card from platform i and the merchant must accept platform i's cards. All consumers and merchants are assumed to hold/accept cash, so cash is always a payment option.
Second, the decision must be made to select that payment method in preference to all other feasible options. Consistent with most treatments of payment systems, this choice at the moment of sale is assumed to fall to the consumer. Each consumer makes this choice to maximise the net benefit he or she will accrue in making that particular payment transaction.
For simplicity, both consumers and merchants are assumed to receive zero utility if cash is used to make a payment. By contrast, as discussed further below, all consumers are assumed to receive non-negative utility from paying by card – so that consumers who hold either platform's card will always prefer to pay by card rather than by cash, if possible.
We now describe the incentives facing: platforms in their choice of pricing strategies; merchants in their decisions whether or not to accept the cards of each platform; and consumers in their decisions whether or not to hold the cards of each platform, and to prefer one or the other – if they hold both – when making any given payment. First, however, it is helpful to introduce some further notation.
2.2 Notation
Let 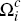 denote the subset of consumers who choose to hold the card of platform i,
and let
denote the subset of consumers who choose to hold the card of platform i,
and let 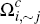 denote the further subset of these consumers who choose not to hold the card of
platform j. Let
denote the further subset of these consumers who choose not to hold the card of
platform j. Let 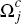 and
and  be defined correspondingly,
and let
be defined correspondingly,
and let 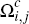 denote the subset of consumers who choose to hold the cards of both platforms i
and j. Finally, let
denote the subset of consumers who choose to hold the cards of both platforms i
and j. Finally, let 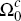 denote the subset of consumers who choose
to hold no cards and use only cash. Clearly we then have that
denote the subset of consumers who choose
to hold no cards and use only cash. Clearly we then have that
and
Next, among those consumers holding both cards it will be necessary to distinguish
also between those who would prefer to use card i over card j, in the event that a merchant accepts the
cards of both platforms, and those who would instead prefer to use card j
over card i. Let 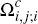 and
and  denote these two subsets
respectively, so that we then also have, in
turn:[5]
denote these two subsets
respectively, so that we then also have, in
turn:[5]
Finally, define  to be the fraction of consumers who choose to hold no cards, and similarly
for
to be the fraction of consumers who choose to hold no cards, and similarly
for 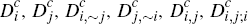 and
and 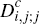 .[6] Corresponding
to Equations (1) to (3) above we then also have that
.[6] Corresponding
to Equations (1) to (3) above we then also have that
and
Turning to the merchant side, let 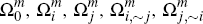 and
and 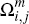 denote the analogous subsets of Ωm (so, for example,
denote the analogous subsets of Ωm (so, for example, 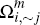 is the subset of merchants who choose to accept the cards of platform i
but not of platform
j).[7]
Then, as for the consumer side, we have the following obvious relationships
is the subset of merchants who choose to accept the cards of platform i
but not of platform
j).[7]
Then, as for the consumer side, we have the following obvious relationships
and
If we again define 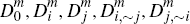 and
and 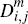 analogously to their consumer counterparts, we then also have the corresponding
identities:
analogously to their consumer counterparts, we then also have the corresponding
identities:
and
For ease of reference, this notation and that introduced in Sections 2.3 to 2.5 below are summarised in Table 1.
| Variable | Description |
|---|---|
| Consumer market segments (fractions) | |
| Ωc | Set of all consumers |
 |
Subset (fraction) of consumers who choose not to hold any cards |
 |
Subset (fraction) of consumers who choose to hold card i |
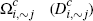 |
Subset (fraction) of consumers who choose to hold card i but not card j |
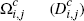 |
Subset (fraction) of consumers who choose to hold both cards i and j |
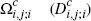 |
Subset (fraction) of consumers who choose to hold both cards and who prefer to use card i over card j whenever merchants accept both |
| Merchant market segments (fractions) | |
| Ωm | Set of all merchants |
 |
Subset (fraction) of merchants that choose not to accept any cards |
 |
Subset (fraction) of merchants that choose to accept card i |
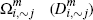 |
Subset (fraction) of merchants that choose to accept card i but not card j |
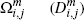 |
Subset (fraction) of merchants that choose to accept both cards i and j |
| Platform fees | |
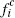 |
Flat fee charged to consumers to subscribe to card i |
 |
The flat fee 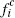 converted to per-transaction terms for
a consumer in converted to per-transaction terms for
a consumer in 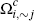 or or 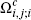 (that is, the
quantity (that is, the
quantity
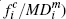 |
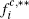 |
The flat fee 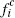 converted to per-transaction terms for
a consumer in converted to per-transaction terms for
a consumer in 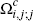 (that is, the quantity (that is, the quantity 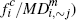 |
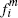 |
Per-transaction fee charged to merchants by platform i |
| Platform costs | |
| ci | Cost incurred by platform i for each transaction processed over the platform |
| gi | Flat cost to platform i of signing up each consumer |
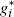 |
The quantity  (representing the flat cost gi
converted to per-transaction terms for subscribers in (representing the flat cost gi
converted to per-transaction terms for subscribers in 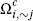 or or 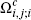 ) ) |
| Other | |
| C (M) | Total number of consumers (merchants) |
| τi | Maximum per-transaction benefit received by any consumer on platform i |
| μi | Maximum per-transaction benefit received by any merchant on platform i |
 |
Per-transaction benefit received by a given consumer on platform i |
 |
Per-transaction benefit received by a given merchant on platform i |
| Πi | Total profit earned by platform i |
| Notes: For simplicity, where there is analogous notation for both platforms only that for platform i is shown. Consumer (merchant) market fractions represent the proportion of all consumers (merchants) that are members of the corresponding set. | |
2.3 Platforms
The two platforms are assumed to be profit-maximising and to face per-transaction costs of ci for platform i and cj for platform j. In addition, they incur fixed costs gi and gj respectively for each consumer that they sign up.
In terms of pricing, we assume that the platforms charge flat fees, 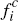 and
and 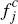 ,
to each consumer, but do not levy per-transaction fees on consumers (nor do
they offer per-transaction rewards). Conversely, platforms do not impose flat,
up-front fees on merchants, but do charge per-transaction fees
,
to each consumer, but do not levy per-transaction fees on consumers (nor do
they offer per-transaction rewards). Conversely, platforms do not impose flat,
up-front fees on merchants, but do charge per-transaction fees 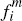 and
and 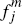 to merchants for the
use of their cards. Thus, for platform i, each consumer that subscribes
generates direct revenue
to merchants for the
use of their cards. Thus, for platform i, each consumer that subscribes
generates direct revenue 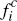 and cost gi, while each
transaction generates revenue of
and cost gi, while each
transaction generates revenue of 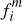 from the relevant
merchant and incurs a processing cost of ci; and similarly
for platform j.
from the relevant
merchant and incurs a processing cost of ci; and similarly
for platform j.
For each platform, profits will be determined by both the number of consumers whom they manage to attract and the volume of transactions subsequently undertaken on the platform. When in competition with one another each platform must, in making its pricing decisions, take into account the expected effects of any fee increases on both consumers and merchants. These effects include causing some consumers (merchants) to abandon the platform in favour of holding (accepting) only cash or the card of the other platform – either as a direct result of the fee impact, or indirectly by reducing the number of merchants prepared to accept the card (consumers wishing to use the card).
Platform i's profit function can be written explicitly as:
The three right-hand-side terms in the top equality of Equation (11) are, respectively: profits from subscriptions; profits from transactions made by cardholders who either only hold card i, or hold both and prefer it over card j; and profits from transactions made by cardholders who prefer card j over card i but hold both.
If we then introduce the further notation – discussed in greater detail below – that
it is readily checked that Equation (11) may alternatively be written
Platform j's profit function is then correspondingly given by
where 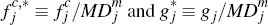 .
.
Sections 3.1 and 3.2 below describe, in greater detail, geometric frameworks for understanding the incentives facing profit-maximising platforms in their fee choices, in terms of the impact of these fee choices on consumers' and merchants' card holding and acceptance decisions.[8]
2.4 Consumers
Consumers make their payment choices so as to maximise their utility. They are assumed
to receive a per-transaction benefit for paying by non-cash means, equal to
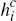 for payments made over network i and
for payments made over network i and 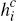 for payments made
over network j. Consumers are heterogeneous in their benefits, which
are randomly (though not necessarily independently) drawn from distributions
over the intervals [0, τi] for platform i
and [0, τj] for platform
j.[9]
for payments made
over network j. Consumers are heterogeneous in their benefits, which
are randomly (though not necessarily independently) drawn from distributions
over the intervals [0, τi] for platform i
and [0, τj] for platform
j.[9]
In Chakravorti and Roson (2006), and in the sequel to this paper (Gardner and Stone 2009a), these distributions are taken to be uniform, as this represents an interesting case and one which significantly simplifies analysis of the model. Consumers' draws of benefits for each platform are also assumed to be independent – so that the benefit any individual consumer receives from making a payment over network i is unrelated to the benefit they receive from making a payment over network j. While it may help the reader to adopt these assumptions mentally in what follows, it is important to note that they are not necessary for the model and, other than in Section 4, we do not require them for the remainder of this paper. Indeed, at the end of Section 2.6 we briefly describe a natural setting in which an alternative joint distributional assumption for consumers' per-transaction benefits might be appropriate.
As noted above, a consumer making a payment over network i or j faces no per-transaction fee. Since each consumer's per-transaction benefit from using either platform is always non-negative, consumers who hold cards will therefore always prefer to pay by card rather than by cash, whenever this is possible. Unlike in Chakravorti and Roson (2006), it is assumed that each consumer can choose to hold no cards, one card or both cards; and, in the event that they sign up to both platforms, can choose to use card i in preference to card j, or vice versa, where a merchant accepts both.
In assessing their expected utility, each consumer is assumed to have a good understanding
of the fraction of merchants who will sign up to each platform, for given
platform fees 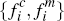 and
and 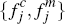 .
The equations which describe the utility a consumer with per-transaction benefits
.
The equations which describe the utility a consumer with per-transaction benefits
 will obtain from each of their possible card holding/use options are thus as follows:
will obtain from each of their possible card holding/use options are thus as follows:
Here, consistent with previous notation, the quantities 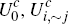 and
and 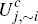 denote the utility the consumer would receive, respectively, from choosing to hold
neither platform's cards, the card of platform i only, or the
card of platform j only. Similarly,
denote the utility the consumer would receive, respectively, from choosing to hold
neither platform's cards, the card of platform i only, or the
card of platform j only. Similarly, 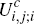 and
and 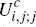 denote the utility
the consumer would receive from choosing to hold both platforms' cards
and then choosing, respectively, to use card i over card j,
or vice versa, whenever a merchant accepts both.
denote the utility
the consumer would receive from choosing to hold both platforms' cards
and then choosing, respectively, to use card i over card j,
or vice versa, whenever a merchant accepts both.
Finally, before turning to the merchant side, it is useful to compute what the effective
charge is, in per-transaction terms, for different consumers who elect to
hold each platform's card. Focusing without loss of generality on the
cards of platform i, we see that consumers in the subsets 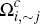 and
and 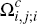 of
of  will each expect to
make
will each expect to
make 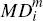 transactions on their platform i cards. Hence, such consumers face an effective
per-transaction charge for these payments of
transactions on their platform i cards. Hence, such consumers face an effective
per-transaction charge for these payments of 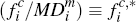 . This provides the
intuitive interpretation for the quantities
. This provides the
intuitive interpretation for the quantities 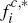 and
and 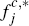 introduced in Section 2.3.
introduced in Section 2.3.
On the other hand, a consumer in the subset 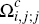 of
of 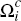 will expect to make only
will expect to make only 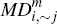 transactions on their platform i
card, since they will use it only when a merchant accepts card i
and does not accept their preferred card j. Hence, these consumers
face a higher effective per-transaction charge for payments on their platform
i
cards than consumers in
transactions on their platform i
card, since they will use it only when a merchant accepts card i
and does not accept their preferred card j. Hence, these consumers
face a higher effective per-transaction charge for payments on their platform
i
cards than consumers in 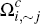 and
and 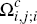 . This effective charge
is
. This effective charge
is
Similarly, consumers in the subset  face a corresponding effective per-transaction cost for payments on their platform
j card of
face a corresponding effective per-transaction cost for payments on their platform
j card of 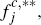 where
where 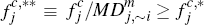 . As we shall see,
the quantities
. As we shall see,
the quantities 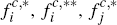 and
and  will play an important
role in the geometric framework described in Section 3.2
for understanding consumers' card holding decisions.
will play an important
role in the geometric framework described in Section 3.2
for understanding consumers' card holding decisions.
2.5 Merchants
Each merchant can choose to sign up to both networks, one network, or neither network,
based on the net benefit it will receive from doing so. Like consumers, merchants
are assumed to receive a per-transaction benefit for accepting non-cash payments,
equal to 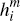 for those received on network i and
for those received on network i and 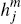 for those received
on network j. Merchants are also heterogeneous in their benefits,
which are randomly (but not necessarily independently) drawn from suitable
distributions over the intervals [0, μi] and [0, μj]
for platforms i and
j.[10].
If a merchant accepts a payment over network i it is charged a per-transaction
fee of
for those received
on network j. Merchants are also heterogeneous in their benefits,
which are randomly (but not necessarily independently) drawn from suitable
distributions over the intervals [0, μi] and [0, μj]
for platforms i and
j.[10].
If a merchant accepts a payment over network i it is charged a per-transaction
fee of 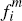 ,
and similarly for platform j. However, merchants do not face any
fixed costs in choosing to accept either platform's cards.
,
and similarly for platform j. However, merchants do not face any
fixed costs in choosing to accept either platform's cards.
In assessing the benefit it will receive from signing up to one or more platforms,
each merchant is once again assumed to have a good knowledge of both: the
fraction of consumers who will sign up to each platform, for given platform
fees 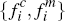 and
and  ;
and the fractions of those choosing to hold both cards who will then prefer
to use a particular card at the moment of sale. Given this, the equations
which describe the net benefit which a merchant, with per-transaction benefits
;
and the fractions of those choosing to hold both cards who will then prefer
to use a particular card at the moment of sale. Given this, the equations
which describe the net benefit which a merchant, with per-transaction benefits
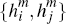 ,will
obtain from each of its possible card acceptance options are as follows:
,will
obtain from each of its possible card acceptance options are as follows:
Once again, the quantities 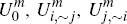 and
and 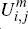 denote the net benefit the merchant would receive, respectively, from choosing to
accept neither platform's cards, the card of platform i only,
the card of platform j only, or those of both platforms. Note that
these equations also rest upon the feature of the model, discussed earlier,
that consumers will always prefer to pay by one or other card rather than
by cash, if possible.
denote the net benefit the merchant would receive, respectively, from choosing to
accept neither platform's cards, the card of platform i only,
the card of platform j only, or those of both platforms. Note that
these equations also rest upon the feature of the model, discussed earlier,
that consumers will always prefer to pay by one or other card rather than
by cash, if possible.
2.6 Possible Applications of the Model
Having specified our ECR model, the next step is to derive descriptions of the aggregate card holding and acceptance behaviour of consumers and merchants in it. Before doing so, however, it is worth briefly addressing the question: to what real-world situations might the model potentially apply?
Since platforms in the model interact directly with participants on both sides of the market, the obvious application is to competition between rival three-party card schemes, such as American Express and Diners Club. The absence of separate issuers and acquirers in the model makes it appropriate to such a setting.
Despite the absence of distinct issuers and acquirers (and consequent lack of explicit interchange fees), the model could arguably still be used to shed light on some features of competition between four-party credit card schemes (such as MasterCard and Visa). While clearly less well adapted to this situation, the model nevertheless accurately captures many features of the dynamics of the consumer and merchant sides of the market which would arise in this setting. It might also offer some insights into competing four-party platforms' likely pricing behaviour, with the tilting of platforms' price structures in favour of consumers or merchants potentially indicative of their likely interchange fee choices in this setting.
That said, caution would need to be exercised before using our ECR model to draw any firm conclusions about the case of competition between four-party schemes. For example, in the event that the issuing side were dominated by a small number of large institutions, the model's applicability to this case would be limited, given its lack of a proper treatment of oligopsony effects (in relation to platforms' pricing behaviour towards such issuers).[11]
Our ECR model potentially also allows us to draw some inferences about the case of competition between different types of payment instrument, such as debit versus credit cards (or cheques versus either of these). Chakravorti and Roson (2006) emphasised the scope for their model to be used to study such competition – stressing, in this regard, its capacity to handle situations where platforms provide different maximum per-transaction benefits to consumers and/or merchants (so τi ≠ τj and/or μi ≠ μj
Our ECR model also offers scope for such differentiation between platforms based on the maximum per-transaction benefits they provide. However, this is not something which we pursue in the simulation analysis in the sequel to this paper. Rather, there is a more fundamental reason why we believe that our ECR model, like Chakravorti and Roson's earlier one, plausibly covers the case of competition between different types of instrument – namely, that it allows for heterogeneous benefits, to both consumers and merchants, across the two competing platforms.
Even where consumers' (merchants' ) benefits from transacting on each platform are uniformly distributed, as long as they are not perfectly correlated then some consumers (merchants) will value using platform i more highly than platform j, and vice versa. This is consistent with the fact that in the real world different agents will, for example, place different intrinsic values on using debit and credit cards. Some consumers, for instance, may be particularly averse to taking on debt, and so appreciate the budgeting discipline provided by a debit card. Others, by contrast, may value the flexibility afforded by a credit card relative to a debit card in managing intra-month cash flow constraints.
Finally, by allowing for non-uniform and/or correlated distributions of consumer and merchant per-transaction benefits across platforms, our ECR model potentially even applies to the case of competition between a premium credit or charge card brand and a non-premium one. To the extent that some consumers might value the prestige associated with holding a certain ‘exclusive’ payment card, this could generate an incentive for one platform to target this market segment – hoping to charge higher fees to cardholders and, if possible, to merchants compared to a rival platform focused instead on increasing profit by maximising its subscriber numbers and transaction volumes. The attraction of such a targeted business approach would be greater, the stronger the concentration of consumers placing an asymmetrically high prestige value on transacting with a premium rather than run-of-the-mill payment instrument. This is something which our ECR model could, in principle, incorporate via using a suitable non-uniform distribution for consumers' per-transaction benefits.[12]
Footnotes
For simplicity, and without impact on the model, we assume that any consumers who
hold both cards, and who would be indifferent between using the two if a
merchant accepted both, are included in the set 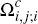 .
[5]
.
[5]
Thus, for example, 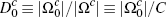 ,
where
,
where  is used to denote the size of a set.
[6]
is used to denote the size of a set.
[6]
Note that there is no need to define analogues of the subsets  and
and 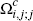 ,
since the choice of payment instrument at the moment of sale is assumed
to fall to the consumer, not the merchant. This makes description of the
merchant side somewhat simpler than that of the consumer side.
[7]
,
since the choice of payment instrument at the moment of sale is assumed
to fall to the consumer, not the merchant. This makes description of the
merchant side somewhat simpler than that of the consumer side.
[7]
The implications of these incentives for platforms' pricing are then explored in Appendix B. [8]
The pairs of quantities 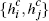 thus typically differ from consumer to consumer but, for each consumer, are the
same for every transaction.
[9]
thus typically differ from consumer to consumer but, for each consumer, are the
same for every transaction.
[9]
As on the consumer side, to fix ideas it may help to focus on the case of uniform and independent distributions throughout the remainder of this paper. Nevertheless, it should again be noted that there is no reason in principle why non-uniform and/or correlated distributions could not be used here. [10]
Another important distinction in the case of competing four-party credit card schemes would be that annual credit card fees are paid by consumers to issuers, rather than to the schemes. We might expect this distinction to have implications for the transferability of any model results regarding how the use of flat fees to consumers, rather than per-transaction fees, would affect platforms' pricing. The importance of this distinction in practice, however, would depend on the extent to which schemes might be able to extract some or all of these flat consumer fees from issuers – say through the use of scheme fees to issuers based on subscriber numbers. [11]
In this way our ECR model might represent an appropriate vehicle for investigating both the presence of premium credit cards in the marketplace alongside more prevalent ordinary credit cards, and the market dynamics of competition between the two. [12]