RDP 2009-02: Competition Between Payment Systems 4. Potential Non-uniqueness of Market Equilibria
April 2009
Sections 3.1 and 3.2 appear to provide complete descriptions of the behaviour of merchants and consumers in our ECR model, for given platform fees. In principle, this should allow us to analyse from a theoretical perspective the factors influencing platforms in their pricing strategies.[21] However, before such an analysis can be undertaken, it turns out that there is a significant issue remaining to be clarified about the geometric frameworks just described.
This issue concerns whether or not, for given fee choices by platforms i and j, the resulting merchant and consumer market outcomes are necessarily uniquely determined. Interestingly, the short answer to this – at least for some fee choices – is no! Moreover, non-uniqueness can arise even for the case where merchant and consumer per-transaction benefits on each platform are uniformly and independently distributed, and where the platforms are identical in their fee choices and the maximum per-transaction benefits they provide to both merchants and consumers.
For this symmetric case it is possible to establish the existence of such non-uniqueness,
as well as identify its extent and the conditions under which it will arise,
purely
analytically.[22]
However, rather than go into the details here we content ourselves with providing
a concrete illustration. This is given by Figure 5, which depicts the case
where τi = τj = τ
and μi = μj = μ,
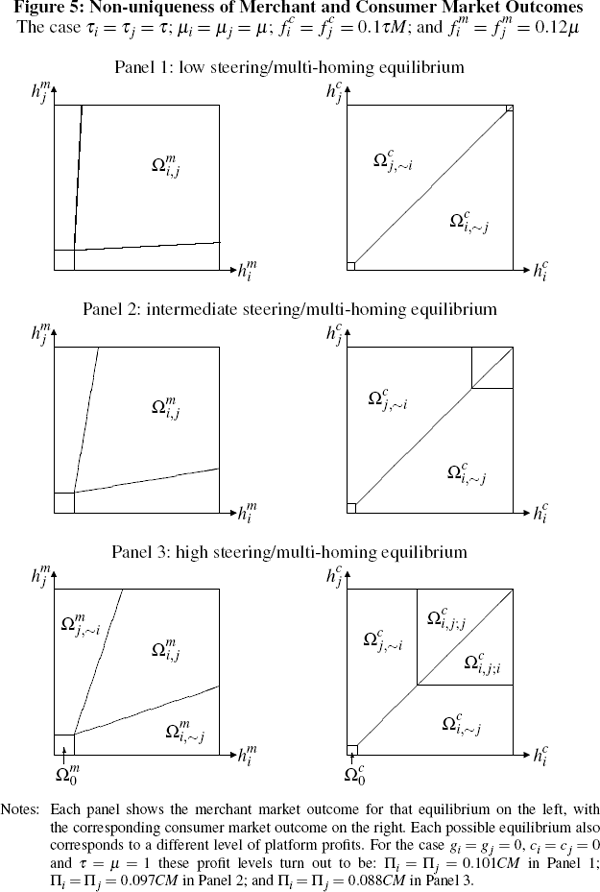
and the platforms set fees 
and 
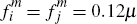. The three panels
in the figure show the three alternative market equilibria which, it transpires,
could arise in this case.
What is the significance of this potential non-uniqueness? We offer two sets of observations. The first set relates to the extent and nature of the non-uniqueness, where it arises. The second concerns its implications for implementing and solving the model numerically, and potentially also for the ‘chicken and egg’ debate about the development of payment systems (and of two-sided markets more generally).
4.1 The Extent and Nature of Non-uniqueness
The first noteworthy feature of the non-uniqueness we observe in our ECR model is that it is not limited to the existence of two possible market equilibria. As Figure 5 demonstrates, at least three (and potentially more) admissible equilibria can arise for some fee choices – even for the case of identical platforms.[23]
This is of interest in view of the most common intuition for how non-uniqueness in market outcomes might occur in payment systems. Known colloquially as the ‘chicken and egg’ effect, it is relevant even in relation to a single payments platform, not just competing platforms. It posits that feedbacks between the merchant and consumer sides might make both ‘high take-up’ and ‘low take-up’ outcomes simultaneously possible, for given platform fees. The former configuration would result if (say) many merchants judged that accepting a platform's cards would be advisable, because of expected high consumer demand. This would then promote exactly the high demand for the platform's cards among consumers that merchants expected, in turn justifying their widespread acceptance of these cards. The latter configuration, also internally consistent, would instead see few merchants judging it likely to be worthwhile to accept a platform's cards, and few consumers choosing to hold these cards, with each side's decisions validating the other's.
In its simplest form, however, this intuition provides a potential rationale for just two distinct market equilibria – rather than the three or more which can arise in our model for some fee settings. Moreover, it is not the case, for the equilibria in our model, that high (low) aggregate card holding by consumers and high (low) aggregate card acceptance by merchants go together. For example, the equilibrium in Panel 1 of Figure 5 involves consumers holding an average of 0.99 cards and merchants accepting an average of 1.76 cards; yet the equilibrium in Panel 3, while having a higher average rate of consumer card holding of 1.32, has a lower average rate of merchant card acceptance of 1.49.
The non-uniqueness in our ECR model is clearly, therefore, of a different character than ‘chicken and egg’ non-uniqueness. Rather, it reflects non-uniqueness in the dimension of merchant steering/consumer multi-homing – with the three panels in Figure 5 corresponding to low, medium and high rates of steering/multi-homing.
Intuitively, the low steering/multi-homing configuration would result if merchants generally expected few consumers to hold multiple platforms' cards. This would lead few merchants to attempt to steer consumers by refusing acceptance of one or other platform's cards, which would then promote exactly the sort of single-homing behaviour by consumers that merchants initially expected. On the other hand, for the same platform fees the high steering/multi-homing outcome would result if merchants instead generally expected most consumers to multi-home. In this case merchants would be much more inclined to steer consumers by accepting only their preferred platform's cards, and this would in turn increase consumers' propensity to multi-home, as initially expected. In the case of Figure 5, both outcomes would be internally consistent and could arise – with each side's decisions validating those of the other – as indeed could an intermediate outcome involving a moderate degree of merchant steering coupled with a corresponding moderate degree of consumer multi-homing.
So far as we know, this form of potential non-uniqueness in market equilibria, for given platform fees, is new and has not previously been concretely illustrated in the literature. Unlike the ‘chicken and egg’ effect, it is relevant only in the context of competing platforms (even where these are symmetric) and cannot arise in a single-platform setting.[24] Its occurrence here illustrates the richness and subtlety of the feedbacks between merchants and consumers in our ECR model.
4.2 The Modelling and Other Implications of Non-uniqueness
The second observation about the potential non-uniqueness in our model is a practical one, namely that it raises the question: for both the monopoly and duopoly settings, to which equilibrium will the market actually settle, where more than one is feasible? Identification of this ‘actual equilibrium’ for every possible set of fee choices is necessary to complete the specification of the model.
The natural decision rule we adopt to resolve any non-uniqueness, at least for the symmetric case, is based on platform profits. Where several potential equilibria are possible for given platform fees, each will correspond to a different profit for each platform. In the case where these profits are symmetric across the two platforms, we assume that it is the common, high-profit equilibrium at which the model settles – consistent with platforms having a profit maximisation objective.[25] This might occur, say, through both platforms providing temporary incentives to consumers and/or merchants to drive the market to this outcome.[26] (The non-symmetric case is obviously more complex and is not dealt with in this paper.[27],[28])
The idea that temporary incentives might be useful to resolve non-uniqueness of merchant and consumer market outcomes may also be relevant to the ‘chicken and egg’ debate in relation to payment systems. The problem of how to get consumers to take up a payment instrument that merchants do not yet widely accept, and vice-versa, is often raised as a key impediment to the development of new payment mechanisms. This has then been used to justify the imposition of interchange fees – or, more generally, pricing skewed in favour of one side of the market – to encourage one side to come on board, thereby promoting take-up by the other side and so overcoming the ‘chicken and egg’ problem.[29]
In its pure form, however, this ‘chicken and egg’ problem is a product entirely of network effect feedbacks between the two sides of the market – exactly as with the non-uniqueness described in Section 4.1. Hence, just as here, if a high take-up equilibrium were deemed preferable to a low one this might justify the temporary use of incentives, such as interchange fees, to shift the market to this equilibrium. However, there would be no need on ‘network effect’ grounds for such incentives to be maintained, once this equilibrium had been achieved; the positive externalities to each side from high take-up on the other would provide sufficient motivation for both consumers and merchants to remain at such an equilibrium. Hence, the case for continuing interchange fees would have to rest on the existence of ongoing usage externalities in the system, generated each time a transaction occurred, as distinct from the sort of ‘usage option’ or membership externalities just discussed.[30]
Footnotes
One such analysis, focusing on the incentives facing a platform contemplating an increase in its flat fee to consumers, is presented in Appendix B. [21]
Details are provided in a separate technical annex: see Gardner and Stone (2009b). [22]
Our theoretical analysis shows that in the symmetric case, for given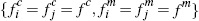 
,
up to six distinct equilibria are potentially feasible. These consist of
one CR solution – by which we mean an equilibrium with no consumers
multi-homing – and up to five others determined by admissible roots
of a quintic polynomial whose coefficients are functions of fc
and fm. If we focus instead on the number of equilibria
for given effective per-transaction fees,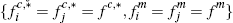 
, we can be even
more precise. In this case, although for many fee settings there will be
a unique equilibrium, for others there can be as many as three distinct
equilibria. If 
these consist of a CR solution and up
to two others involving some consumer multi-homing, determined by admissible
roots of a cubic polynomial whose coefficients are functions of fc,*
and fm; if 
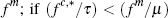they consist of
up to three equilibria involving consumer multi-homing, determined by admissible
roots of this same cubic. Full details are provided in Gardner and Stone
(2009b).
[23]
Indeed, the only other paper of which we are aware that discusses non-uniqueness of merchant and consumer market outcomes at any length, other than in the ‘chicken and egg’ sense, is Armstrong and Wright (2007). They consider a model in which various assumptions ensure that agents on one side will all single-home, regardless of the pricing they face. They then find that four different, internally consistent, market equilibria can potentially arise for given platform prices (although at most, three can ever be feasible simultaneously). No market outcome is possible, however, in which some but not all agents on one side multi-home. This accounts for why Armstrong and Wright's framework does not generate the sort of non-uniqueness identified above for our ECR model (corresponding to different gradations of aggregate consumer multi-homing/merchant steering). [24]
In the case of Figure 5, for example, this is the ‘low steering/multi-homing’ equilibrium shown in Panel 1 of the figure. [25]
Such incentives would not necessarily require collusion between platforms – something which would be inconsistent with competition in the duopoly setting – since both platforms' interests are aligned in the symmetric case. [26]
Since platforms in this situation might order feasible equilibria differently by profit, some mechanism would be required to determine which potentially second-best outcome for both platforms would actually be arrived at in this case. One possibility would be a game-theoretic procedure that would sit within the broader competitive game facing each platform of choosing its fees so as to maximise its profits, while taking into account how the other platform might respond. For the general non-symmetric case we do not pursue this ‘game within a game’ issue further here. [27]
For the special non-symmetric case of small perturbations away from a symmetric fee setting we adopt a different approach altogether, in the sequel to this paper (Gardner and Stone 2009a), to resolving any potential non-uniqueness. In such cases we assume that the actual market equilibrium will be the one reached by starting from the symmetric equilibrium and then iteratively adjusting the merchant and consumer sides of the market, in turn, in the manner described in Appendix B of this paper, until these cease changing. This sort of iterative procedure is actually the same as that used in Roson (2005) to carry out simulation analyses – although we use it only for the case of infinitesimal perturbations from a symmetric solution. [28]
We leave aside here the issue of whether growth of a new payment mechanism need always be welfare-improving. [29]
For a more detailed discussion of membership versus usage externalities in payment systems (and two-sided markets more generally) see Rochet and Tirole (2005). [30]