RBA Annual Conference – 1995 Problems in the Measurement and Performance of Service-Sector Productivity in the United States Robert J. Gordon
1. Introduction
In the past two decades, the American economy has evolved quite differently from most other advanced industrialised economies. Unlike economies which have experienced a large increase in unemployment, the US unemployment rate in 1994–95 has been little different than in other prosperous years, such as 1972, 1979, and 1987–88. Instead, there is now a general consensus that the most intractable problems of the American economy are slow growth in productivity and in real wages. Productivity growth has proceeded at barely one per cent per year since 1972, and growth in real wages for most employed persons has been less than that, due to an increase in inequality that has concentrated much of the limited payoff from productivity growth in the top 20 per cent of the income distribution.
When examined more closely, it appears that America's productivity performance is characterised by a dichotomy. Subject to several measurement caveats to be explained below, the performance of American manufacturing has been quite robust, with 1987–94 growth in output per hour of 2.9 per cent, more rapid than the 2.6 per cent rate recorded during productivity's golden age of 1950–72, and much more rapid than the 2.2 per cent rate of the dark age during the intervening period, 1972–87. It is in non-manufacturing, mainly the services, that the problem of slow productivity growth and the post-1972 growth slowdown is concentrated. The corresponding growth rates for private non-farm non-manufacturing (PNFNM) over 1950–72, 1972–87, and 1987–94 are, respectively, 2.1, 0.4 and 0.8 per cent per annum. And, as we shall see, growth for the PNFNM sector of multi-factor productivity (which differs from output per hour by factoring out the contribution of capital input) has been barely positive since 1972.
1.1 Substantive and Measurement Issues
How is slow productivity growth in the American non-manufacturing sector to be explained? A number of explanations have been proposed and several of these, like the oil price shocks of the 1970s, have been discarded as the poor productivity performance grinds on inexorably while the shock in question has disappeared. We shall review the evidence on several traditional explanations, including inadequate saving and investment, a decline in labour quality, a deteriorating infrastructure, and the depletion of resources and ideas. We shall investigate problems of particular industries that suggest pockets of difficulty rather than an economy-wide malaise. And, as a final potential cause, we shall suggest the possibility that the vaunted flexibility of the American labour market contributes to the productivity problem – weak unions, a drastic decline in the real minimum wage, and lax immigration barriers combine to foster an ample supply of low-wage labour that, in turn, encourages American employers to overstaff particular service occupations compared with their counterparts in other countries.
But before searching for explanations, we need to confront a suspicion that perhaps the phenomenon to be explained does not exist. Some writers have claimed that productivity growth has been rapid rather than slow, and that a complex set of measurement errors has prevented the true achievements of the American economy from being adequately captured by the official data. They argue that there has been an explosion of new technology over this period, especially in computers and electronics. They point to examples of industries that have transformed their operations and raised efficiency. They (especially Griliches (1994)) point to a steadily rising fraction of output produced in industries in which output is intrinsically hard to measure.
With Martin Baily, l have examined the relation between the measurement of productivity and the productivity slowdown in the United States and asked whether measurement errors could account for much or all of the post-1972 productivity slowdown (Baily and Gordon 1988). We concluded that they could not, for two basic reasons. First, a measurement error can ‘explain’ the slowdown only to the extent that the error became worse or had a bigger impact in the slowdown period than it did in prior periods. Thus, the failure of standard price data to capture the improvement in the quality of many outputs (leading to an understatement of real output) can only explain the slowdown to the extent that quality change has proceeded more rapidly in recent years than it did before l973. A second reason for the small impact of measurement errors in explaining the slowdown is that many of these errors occur in industries that partly or wholly produce intermediate goods. In the United States, the computation of GDP starts with aggregate data on final shipments and sales of consumption, investment and government goods and net exports. This total is then allocated down to the sectors, as GDP originating by industry. Errors in the computation of, say, GDP originating in the trucking industry will alter the fraction of total private GDP that is thought to be generated in this industry, but not the estimate of total GDP. If trucks are really producing more real output than we thought, then the industries that buy trucking services are producing less.
While measurement errors cannot explain the entire slowdown, or why PNFNM productivity growth falls short of that in most other OECD nations, nevertheless the errors are sufficiently important that a full set of corrections could easily double the recorded rate of PNFNM productivity growth in the United States. In this paper, I take another look at the wide variety of measurement issues that must be confronted in assessing productivity in the services, and this reassessment convinces me that Baily and Gordon (1988) understated the seriousness of measurement errors. My new verdict relies primarily on several sources of upward bias in the American consumer price index (CPI) that have been identified since 1988 by government statisticians within the Bureau of Labor Statistics (BLS) and which imply a corresponding downward bias in the growth rate of output and productivity within the US service sector.
The measurement problems discussed in this paper are relatively complex, and some of them may not apply in every other country. The United States is almost unique in using a hedonic price index for the output of electronic computers and then introducing that deflator into the national accounts and productivity statistics with a weighting scheme that is highly inappropriate. The result is that all official output and productivity data for the US for sectors or aggregates including the computer-producing industry (including manufacturing and GDP as a whole) substantially understate performance prior to 1987 (the base year in the current US national accounts) and overstate performance since 1987. Correction for this ‘base-year index bias’ raises the hurdle that the economy must surpass for us to conclude that the productivity-growth slowdown of the past two decades has abated.
1.2 Plan of the Paper
The paper begins with several tables that document the magnitude of the productivity-growth problem within the United States, both in the aggregate and for sub-industries, and which compare US performance with that in several other large nations. We then turn to the measurement issues, distinguishing those that involve the measurement of current-dollar output, price deflators, and hours of labour input. The last part of the paper investigates substantive causes of the weak productivity performance in the services, with special emphasis on problems experienced by particular industries.
2. US Productivity Performance in the Official Data
Our presentation of official data in this section emphasises the contrast between the performance of the manufacturing and PNFNM sectors in the US. It also examines differences among the US and other members of the G7 countries in the behaviour of productivity at the aggregate and sectoral level.
2.1 Productivity Behaviour Within the American Economy
Table 1 displays the annual average growth rates over specified intervals of output per hour (hereafter average labour productivity or ALP) and multi-factor productivity (MFP). The dividing points between the intervals are chosen to be periods when the economy was at roughly a neutral level of demand pressure, with an unemployment rate in the range of 5.5–6.0 per cent. Thus differences in performance across intervals are not influenced by cyclical movements in productivity. The right-hand column computes the overall slowdown in productivity growth between the first two intervals, covering 1950–72, and the second two intervals, covering 1972–94.
| 1950:2– 1963:3 |
1963:3– 1972:2 |
1972:2– 1987:3 |
1987:3– 1994:4 |
Slowdown 1972–94 minus 1950–72 |
|
|---|---|---|---|---|---|
| Output per hour | |||||
| Non-farm business | 2.36 | 2.13 | 0.99 | 1.24 | −1.13 |
| Manufacturing | 2.60 | 2.53 | 2.13 | 2.90 | 0.00 |
| Non-farm non-manufacturing business | 2.25 | 1.92 | 0.50 | 0.76 | −1.46 |
| Multi-factor productivity | |||||
| Non-farm business | 1.42 | 1.09 | 0.32 | 0.90 | −0.65 |
| Manufacturing | 1.70 | 1.37 | 1.29 | 2.51 | 0.37 |
| Non-farm non-manufacturing business | 1.34 | 0.96 | −0.02 | 0.41 | −0.96 |
Looking first at the aggregate economy (the private non-farm or NFP sector), we note the substantial slowdown in ALP growth from 2.25 per cent in 1950–72 to just 0.99 per cent during 1972–87 and l.24 per cent for 1987–94. As we shall see, the apparent recovery after 1987 is illusory and is influenced by the base-year index bias involving computers. In manufacturing there has been an even healthier revival after 1987 and no post-1972 slowdown at all, but (since computers are a larger share of manufacturing than of the aggregate economy) the base-year index bias is larger for manufacturing than for the aggregate. In the large non-manufacturing sector (PNFNM) there has been an even sharper ALP growth slowdown than for the aggregate economy.
The bottom section of Table 1 exhibits growth rates of MFP for the same sectors and time intervals. Because the growth rate of capital input slowed in the final 1987–94 period relative to earlier periods, MFP growth slowed less in absolute terms than ALP. Stated another way, a slower rate of capital accumulation explains a portion of the observed slowdown in ALP growth. And, for the same reason, in the manufacturing sector MFP growth accelerates after 1987 to the most rapid rate observed in any of the intervals shown.
2.2 International Comparisons
Does the abysmal performance of PNFNM productivity in the United States have any counterpart in the rest of the G7 countries? Is there the same dichotomy between manufacturing and PNFNM elsewhere? Table 2 arrays the G7 countries plus Australia in eight columns and separates the sample period into three intervals – 1960–73, 1973–79, and 1979–92. This table begins by covering three aggregates, all private industry, PNF and PNFNMNM (this stands for private non-farm non-manufacturing non-mining). On subsequent pages are arrayed nine sectors for which roughly comparable data are available across the G7 countries: agriculture, mining, manufacturing, construction, utilities, transport/communication, trade, finance, insurance and real estate, and services.
| US | Australia | Canada | Japan | France | Germany | Italy | UK | |
|---|---|---|---|---|---|---|---|---|
| Private industry | ||||||||
| 1960–73 | 1.97 | — | 3.25 | 9.36 | 5.70 | 5.75 | 7.91 | 3.70 |
| 1973–79 | 0.42 | 1.88 | 1.30 | 3.29 | 4.27 | 4.59 | 2.99 | 2.23 |
| 1979–92 | 1.27 | 1.92 | 1.43 | 3.60 | 2.89 | 2.53 | 2.31 | 2.26 |
| Private non-farm | ||||||||
| 1960–73 | 1.92 | — | 3.02 | 8.27 | 4.90 | 5.32 | 6.58 | 3.53 |
| 1973–79 | 0.46 | 1.58 | 1.27 | 3.14 | 3.94 | 4.39 | 2.46 | 2.20 |
| 1979–92 | 1.18 | 1.83 | 1.41 | 3.25 | 2.55 | 2.34 | 1.88 | 2.18 |
| Private NFNMNM(b) | ||||||||
| 1960–73 | 1.34 | — | 2.38 | 7.50 | 3.85 | 4.80 | 6.01 | 2.77 |
| 1973–79 | 0.45 | 1.46 | 1.81 | 1.51 | 3.25 | 4.39 | 1.76 | 1.43 |
| 1979–92 | 0.64 | 1.85 | 1.35 | 2.63 | 2.33 | 2.47 | 0.67 | 1.11 |
| Agriculture | ||||||||
| 1960–73 | 2.66 | — | 6.03 | 7.66 | 6.70 | 6.96 | 8.89 | 7.06 |
| 1973–79 | −1.68 | 5.20 | 0.92 | 0.64 | 5.35 | 5.97 | 4.69 | 2.71 |
| 1979–92 | 5.19 | 2.37 | 2.17 | 2.95 | 6.23 | 5.28 | 4.10 | 5.34 |
| Mining(c) | ||||||||
| 1960–73 | 3.05 | — | 3.50 | 13.92 | 4.20 | 3.81 | — | 5.56 |
| 1973–79 | −10.22 | 2.64 | −7.19 | 6.00 | 4.23 | 0.87 | — | 17.28 |
| 1979–92 | 4.46 | 2.88 | 1.73 | 4.20 | 3.02 | 0.14 | — | 7.60 |
| Manufacturing(c)(d) | ||||||||
| 1960–73 | 3.28 (3.27) |
— | 4.13 | 10.43 | 6.90 | 5.88 | 6.52 | 4.60 |
| 1973–79 | 0.90 (0.52) |
2.76 | 1.77 | 6.34 | 4.98 | 4.44 | 3.86 | 1.64 |
| 1979–92 | 2.50 (2.17) |
2.78 | 2.10 | 3.94 | 2.85 | 2.05 | 3.49 | 4.42 |
| Construction | ||||||||
| 1960–73 | −2.37 | — | 2.08 | 7.05 | 3.45 | 4.42 | 4.72 | 2.61 |
| 1973–79 | −1.53 | 2.67 | 0.01 | 0.08 | 1.78 | 2.76 | 1.00 | 0.48 |
| 1979–92 | 0.09 | −0.22 | 2.03 | 2.40 | 2.96 | 1.55 | 1.03 | 1.68 |
| Utilities | ||||||||
| 1960–73 | 4.43 | — | 5.68 | 6.23 | 7.46 | 7.00 | 6.17 | 6.89 |
| 1973–79 | −0.24 | 2.65 | 3.50 | 4.17 | 5.37 | 6.26 | 0.62 | 3.16 |
| 1979–92 | 0.56 | 5.79 | 0.32 | 4.04 | 4.52 | 2.21 | 1.61 | 4.45 |
| Transportation/Communication | ||||||||
| 1960–73 | 3.68 | — | 4.62 | 7.18 | 5.09 | 4.80 | 4.87 | 4.96 |
| 1973–79 | 2.72 | 4.86 | 2.88 | 2.22 | 3.98 | 6.28 | 3.31 | 2.22 |
| 1979–92 | 2.99 | 4.71 | 3.82 | 3.40 | 4.21 | 3.62 | 2.65 | 3.62 |
| Trade | ||||||||
| 1960–73 | 2.05 | — | 3.26 | 8.88 | 3.69 | 4.67 | 7.06 | 2.89 |
| 1973–79 | 0.64 | 0.77 | 0.85 | 2.24 | 3.21 | 3.64 | 2.05 | −0.03 |
| 1979–92 | 2.22 | 0.66 | 1.04 | 3.83 | 1.58 | 1.66 | 0.79 | 1.59 |
| Finance, insurance and real estate(e) | ||||||||
| 1960–73 | 1.20 | — | 1.12 | 7.15 | 1.70 | 2.70 | — | 0.54 |
| 1973–79 | 0.49 | −0.33 | 1.40 | 3.11 | 2.27 | 4.08 | — | 1.97 |
| 1979–92 | 0.43 | −0.25 | 1.17 | 2.25 | 0.45 | 2.24 | — | 0.00 |
| Services(e) | ||||||||
| 1960–73 | 1.36 | — | 1.35 | 7.71 | 2.54 | 4.45 | 4.61 | 1.04 |
| 1973–79 | 0.41 | 0.92 | 2.74 | −0.64 | 1.92 | 3.80 | 0.51 | 0.42 |
| 1979–92 | −0.68 | 0.52 | 0.36 | 1.47 | 2.47 | 2.46 | −1.26 | −2.51 |
| Notes: (a) Canadian data are available from 1961–92, Japanese data
from 1962–92, and German data from 1962–91. (b) NFNMNM stands for private non-farm, non-mining, non-manufacturing. (c) Italian mining and manufacturing are aggregated and the growth rate is given in manufacturing. (d) US manufacturing growth rates are shown with and without computers, respectively. (e) Italian finance, insurance and real estate are included in services. |
||||||||
For the purposes of this paper, we are most interested in the magnitude of the productivity growth slowdown across countries and the extent to which there is a dichotomy in other countries between the behaviour of the manufacturing and non-manufacturing sectors. Looking first at the PNF sector, we note that every country experienced a substantial post-1973 slowdown in productivity growth, and that the slowdown in the US was actually the smallest in absolute magnitude when 1960–73 is compared with l979–92. Several countries, particularly France, Germany, and the UK, performed worse in 1979–92 than in the oil-shock period of 1973–79, in contrast to the US which performed better.
A surprising result is found when productivity growth rates are compared over the same intervals for the PNFNMNM sector. Productivity growth in this sector over 1979–92 was almost as slow in Italy and the UK as in the US, but was much more rapid in Japan, France and Germany. As is true in most of the comparisons in these tables, the absolute magnitude of the slowdown between 1960–73 and 1979–92 was least in the US and much greater in Japan and Italy.
Turning now to the manufacturing sector, the numbers in parentheses (available for the US only) provide a measure for manufacturing excluding the 2-digit industry that makes computers. This omission makes a substantial difference and drops the US performance to the bottom of the league table (tied, surprisingly, with Germany). Of particular note is the enormous revival of UK manufacturing performance after 1979 to the top of the league table, ahead even of Japan.
Several points should be emphasised about productivity in US manufacturing. First, the official data record a growth rate of 4.1 per cent for 1992–94, which pushes the 1979–94 average growth rate up from 2.5 to 2.7 per cent. While this performance is quite respectable in comparison with that registered by Canada, France and Germany, it is nonetheless tainted by base-year index bias. While no official data exist on the base-year index bias for the manufacturing sector, as we shall see below the bias is about 0.55 per cent for total GDP in 1992–94 and is doubtless larger than that for manufacturing. A second point is that, even including allowance for the base-year index bias, US manufacturing (unlike the US service sector) does not represent an outlier with extraordinarily poor performance that needs to be explained.
We now turn to the performance of the six components of the PNFNMNM portion of the US economy, representing about three-quarters of private-sector output. Two problem cases are listed in Table 2. The productivity performance of the US construction industry is a much-discussed but little-understood oddity. Productivity growth was sharply negative between the early 1960s and the late 1970s and barely positive since then. The construction sector is a prime suspect for major measurement errors; the ratio of US to Canadian productivity level in construction falls over the past three decades by two-thirds, which seems highly implausible.
Listed next is the utility sector, comprising electricity, gas and water. Here the growth rate of US productivity has been barely positive since 1973, and the post-1973 slowdown was the greatest of any sector listed in Table 2. And the performance of US productivity in the utilities sector is exceedingly poor in comparison with all the other G7 countries, with the exception of Canada after 1979. The final section of the paper suggests that the experience of the utilities sector supports the technological depletion hypothesis (‘running out of ideas’).
Next is the transportation and communications sector. (Data are available for these two sectors separately for the US but the two sectors must be combined for international comparisons.) The relatively favourable performance of the US combines an outstanding record for the telecommunications and railroad subsectors with mediocre performance by airlines and trucking.
Also listed are the remaining components of the non-manufacturing sector. In trade the US enjoyed a substantial recovery after 1979, and exhibits no productivity growth slowdown when l979–92 is compared with 1960–73. In fact, the US performance in trade exceeds that in any other G7 country besides Japan. As we shall see, the average performance for US trade disguises highly divergent behaviour in individual parts of the retail sector.
Finance, insurance and real estate represents one of the worst-performing US sectors and one where measurement issues are paramount. The post-1973 growth slowdown for the US is not particularly large (in contrast to utilities), because the pre-1973 growth performance was poor as well. The cross-country comparison reveals substantial heterogeneity and negative productivity growth in the UK after 1979.
The final section of Table 2 covers miscellaneous services. This large sector, representing 22 per cent of US private GDP in 1991, lies at the heart of the US productivity growth problem. The largest single subsector of services is the health service sector comprising about 7 per cent of private GDP, and this sector is subject to severe measurement problems. Nevertheless, the US is not unique in having poor productivity growth in the services sector. Italy and the UK also display virtually no growth in services productivity since 1973 and Canada virtually none since 1979.
Overall, the performance of the US economy is poor by international standards and also highly heterogeneous. The US is at or near the top of the league table only in agriculture, mining and telecommunications. Performance in manufacturing and trade is roughly average, while the major problem areas appear to be construction (4.6 per cent of 1991 GDP), utilities (3.4 per cent), finance, insurance and real estate (20.8 per cent) and services (21.8 per cent).
2.3 Productivity Performance at the Detailed Industry Level
The US statistical system provides three sets of information on productivity at the detailed industry level. First, the national income and product accounts (NIPA) contain detailed output data for about 75 industries, but hours worked data for only a small subset of these. Second, productivity defined as output per person engaged (including both employees and self-employed persons) can be calculated for the full set of 75 industries. Third, the BLS compiles a separate set of output per hour and per employee data for selected industries; however these are not aggregated in a form comparable to the NIPA data.
We turn first in Table 3 to the industries for which NIPA hours data are available. This provides additional detail beyond that available in Table 2. We note the outstanding productivity record since 1979 of the farming and communications sectors. Farming has experienced a substantial acceleration of productivity growth since 1979, as has construction (in the sense that the period of rapid productivity decline seems to have ended). The detail in Table 3 also indicates that the favourable performance of manufacturing is occurring in the durable goods sector, and that non-durable goods manufacturing did not perform well after 1987.
| 1960–72 | 1972–79 | 1979–87 | 1987–92 | Slowdown 1979–92 minus 1960–72 |
|
|---|---|---|---|---|---|
| Private industries | 2.04 | 0.53 | 1.32 | 1.19 | −0.79 |
| Agriculture, forestry and fisheries | 3.30 | −2.15 | 5.52 | 4.64 | 1.78 |
| Farms | 4.20 | −1.56 | 7.26 | 6.32 | 2.59 |
| Agricultural services, forestry and fisheries | −3.07 | −2.81 | 3.44 | 2.99 | 6.28 |
| Mining | 3.55 | 0.53 | 5.36 | 3.01 | 0.64 |
| Construction | −1.70 | −2.81 | −0.24 | 0.61 | 1.88 |
| Manufacturing | 3.16 | 1.43 | 2.67 | 1.99 | −0.83 |
| Durable goods | 3.00 | 0.58 | 2.73 | 2.82 | −0.22 |
| Non-durable goods | 3.39 | 2.68 | 2.54 | 0.87 | −1.68 |
| Transportation and public utilities | 3.75 | 2.09 | 2.20 | 2.43 | −1.43 |
| Transportation | 3.14 | 1.76 | 1.67 | 2.40 | −1.10 |
| Communication | 4.77 | 4.27 | 5.28 | 4.09 | −0.09 |
| Electricity, gas and sanitary services | 4.04 | 1.10 | −0.05 | 1.54 | −3.29 |
| Wholesale trade | 3.24 | 1.39 | 4.27 | 1.80 | −0.20 |
| Retail trade | 1.55 | 0.37 | 1.69 | 1.38 | −0.02 |
| Finance, insurance and real estate | 1.32 | 0.39 | −0.80 | 2.41 | −0.51 |
| Services | 1.37 | 0.53 | −0.67 | −0.68 | −0.24 |
A more detailed industry breakdown is available in Table 4, where productivity is defined as output per person engaged, not per hour. Since the focus of this paper is on the service sectors, we will skip over the first page of Table 4 and focus on the second page. In the transportation sector we note the superb record of the railroad industry since its deregulation in 1980. The largest component of transportation, the trucking industry, was also deregulated in the early 1980s but did not experience a productivity revival until after 1987. The airline industry was deregulated in stages between 1978 and 1981, but its productivity steadily decelerated in each successive period in Table 4.
| 1960–72 | 1972–79 | 1979–87 | 1987–92 | Slowdown 1979–92 minus 1960–72 |
|
|---|---|---|---|---|---|
| Total economy | 2.01 | 0.22 | 0.68 | 0.84 | −1.25 |
| Private industries | 2.21 | 0.07 | 1.04 | 0.94 | −1.22 |
| Agriculture, forestry & fisheries | 3.43 | −0.46 | 4.86 | 4.94 | 1.47 |
| Farms | 3.91 | 0.14 | 6.40 | 5.83 | 2.21 |
| Agricultural services, forestry & fishery | −1.15 | −2.90 | 1.87 | 3.86 | 4.38 |
| Mining | 4.15 | −9.14 | 5.31 | 3.68 | 0.34 |
| Metal mining | 1.47 | −3.81 | 16.17 | 18.83 | 16.03 |
| Coal mining | 3.57 | −6.19 | 10.63 | 10.89 | 7.19 |
| Oil and gas extraction | 4.60 | −12.24 | 3.28 | 0.96 | −2.48 |
| Nonmetallic minerals, except fuels | 4.02 | −0.07 | 2.02 | 1.40 | −2.31 |
| Construction | −1.93 | −2.64 | −0.50 | 0.26 | 1.81 |
| Manufacturing | 3.11 | 1.12 | 2.77 | 2.00 | −0.73 |
| Durable goods | 2.97 | 0.31 | 2.82 | 2.76 | −0.18 |
| Lumber and wood products | 4.99 | 0.44 | 4.23 | −3.01 | −4.38 |
| Furniture and fixtures | 2.48 | 0.65 | 3.16 | 0.69 | −0.56 |
| Stone, gas, and glass products | 2.53 | 0.15 | 1.49 | 2.58 | −0.49 |
| Primary metal industries | 1.96 | −1.84 | 1.74 | 1.53 | −0.33 |
| Fabricated metal products | 2.44 | 0.51 | 2.84 | 1.34 | −0.36 |
| Machinery, except electrical | 2.71 | −0.51 | 2.79 | n.a. | 1.33 |
| Industrial machinery, and equipment | n.a. | n.a. | n.a. | 5.28 | — |
| Electric and electronic equipment | 5.04 | 3.61 | 4.66 | n.a. | 0.20 |
| Electronics and other electronic equipment | n.a. | n.a. | n.a. | 5.81 | — |
| Motor vehicles and equipment | 4.13 | 1.13 | 1.56 | −1.85 | −4.28 |
| Other transportation equipment | 2.55 | −1.14 | 3.92 | 1.49 | 0.15 |
| Instruments and related products | 3.47 | 1.77 | 1.49 | 6.39 | 0.47 |
| Miscellaneous manufacturing industries | 3.36 | −0.68 | 4.56 | 2.25 | 0.05 |
| Non-durable goods | 3.31 | 2.32 | 2.64 | 0.95 | −1.52 |
| Food and kindred products | 3.37 | 2.06 | 3.65 | 0.81 | −1.14 |
| Tobacco manufactures | 3.47 | 2.64 | −2.38 | −7.44 | −8.38 |
| Textile mill products | 5.67 | 5.17 | 4.04 | 3.65 | −1.83 |
| Apparel and other textile products | 2.44 | 4.30 | 2.50 | 3.50 | 0.56 |
| Paper and allied products | 3.23 | 2.33 | 2.20 | 2.21 | −1.03 |
| Printing and publishing | 2.07 | 0.54 | −1.01 | −1.51 | −3.33 |
| Chemicals and allied products | 5.19 | 1.47 | 4.03 | 0.26 | −3.05 |
| Petroleum and coal products | 4.07 | 0.88 | 5.52 | 0.34 | −1.14 |
| Rubber and miscellaneous plastics products | 7.56 | 1.60 | 4.69 | 2.67 | −3.88 |
| Leather and leather products | 2.11 | 2.08 | 3.21 | 6.19 | 2.59 |
| Transportation and public utilities | 3.81 | 1.70 | 2.06 | 2.38 | −1.59 |
| Transportation | 3.13 | 1.04 | 1.53 | 2.37 | −1.18 |
| Railroad transportation | 4.48 | 3.15 | 9.48 | 7.15 | 3.84 |
| Local and interurban passenger transit | −2.45 | −1.94 | −3.03 | −2.10 | −0.11 |
| Trucking and warehousing | 3.99 | 0.12 | 0.22 | 3.60 | −2.08 |
| Water transportation | 2.62 | 2.71 | 0.03 | −0.20 | −2.71 |
| Transportation by air | 4.48 | 3.02 | 2.19 | 1.35 | −2.71 |
| Pipelines, except natural gas | 8.70 | −1.38 | 0.17 | −2.68 | −9.96 |
| Transportation services | −1.43 | 0.13 | 0.05 | −0.08 | 1.41 |
| Communication | 4.91 | 4.60 | 5.12 | 4.06 | −0.32 |
| Telephone and telegraph | 5.85 | 5.15 | 6.46 | 4.65 | −0.30 |
| Radio and television | −1.01 | 1.37 | −2.61 | 3.92 | 1.67 |
| Electric, gas, and sanitary services | 4.22 | 0.85 | −0.07 | 1.54 | −3.49 |
| Wholesale trade | 3.58 | 0.94 | 3.97 | 1.72 | −0.74 |
| Retail trade | 1.92 | −0.56 | 1.03 | 1.20 | −0.81 |
| Finance, insurance, and real estate | 1.39 | −0.16 | −0.92 | 1.73 | −0.99 |
| Banking | −0.01 | 0.02 | 0.00 | n.a. | 0.01 |
| Depository institutions | n.a. | n.a. | n.a. | 0.00 | — |
| Credit agencies, other than banks | 0.11 | 0.02 | 0.02 | n.a. | −0.13 |
| Non-depository institutions | n.a. | n.a. | n.a. | −0.06 | — |
| Security and commodity brokers | 0.02 | 1.47 | 0.71 | 6.32 | 3.49 |
| Insurance carriers | 1.73 | 0.44 | −3.18 | 5.92 | −0.37 |
| Insurance agents, brokers, and service | 0.64 | −4.08 | 6.68 | −0.83 | 2.29 |
| Real estate | 1.74 | −1.68 | −2.89 | 1.42 | −2.47 |
| Holding and other investment offices | 0.01 | −0.83 | −0.02 | 0.37 | 0.17 |
| Services | 1.26 | 0.04 | −0.68 | −0.89 | −2.04 |
| Hotels and other lodging places | 0.76 | −0.46 | −0.91 | 4.04 | 0.81 |
| Personal services | 1.88 | −1.47 | −0.97 | −1.20 | −2.86 |
| Business services | −0.22 | −0.48 | −0.75 | −0.96 | −0.63 |
| Auto repair, services, and parking | 2.67 | −0.27 | −2.25 | −1.77 | −4.68 |
| Miscellaneous repair services | 0.01 | 0.15 | −1.07 | −0.25 | −0.67 |
| Motion pictures | 0.62 | 2.02 | 1.81 | −4.48 | −1.96 |
| Amusement and recreation services | −1.16 | 0.83 | 2.43 | 2.16 | 3.46 |
| Health services | 0.65 | −0.73 | −1.26 | −2.36 | −2.46 |
| Legal services | 1.14 | −3.75 | −3.72 | 0.55 | −2.72 |
| Educational services | −0.04 | −0.10 | −0.69 | 1.06 | 0.22 |
| Social services and membership organisations | 0.17 | −0.09 | −0.31 | −0.52 | −0.58 |
| Miscellaneous professional services | 1.24 | −1.98 | −0.79 | n.a. | −2.10 |
| Other services | n.a. | n.a. | n.a. | −0.92 | — |
| Private households | −0.88 | 1.60 | 0.49 | 0.82 | 1.54 |
Considerable detail is provided for the components of the finance, insurance and real estate sector. Banking and depositary institutions experienced no productivity growth throughout the post-war period, but as we shall see that reflects a measurement issue rather than reality. There were substantial post-1987 improvements in the performance of securities and commodities brokers, of insurance carriers, and of the large real estate industry, but a poor performance by insurance agents.
Within the services sector, the weakest performances occur in personal services, business services, auto repair, health services and legal services (the latter for 1972–87). The only strong performances are in hotels (after 1987) and amusement and recreation services.
A different set of industry productivity indices is provided by the BLS. In some cases the underlying source of output data differs from that in the NIPA data summarised in Tables 3 and 4. In general, the BLS uses gross output rather than value-added as its output concept, and it relies more on measures of physical volume, whereas the NIPA output data are mainly based on double-deflated value-added (and thus more prone to error if deflators are erroneous or inconsistent). The BLS series also provide considerable detail within the retailing sector not available in the NIPA.
Table 5 provides annual growth rates of output per hour for the BLS industries outside of manufacturing. Only a single time period is presented here, 1973–92. Comparing Tables 4 and 5 for the transportation sector, we emerge with a consistent story except for trucking, where the BLS records substantially more rapid productivity growth than in the NIPA.[1] In the utility sector there is the same stark contrast in Table 5 as in Tables 3 and 4 between the telecommunications industry and the other utilities.
| 1973–1992 | |
|---|---|
| Transportation | |
| Railroad transportation, revenue traffic | 6.0 |
| Railroad transportation, car miles | 3.8 |
| Bus carriers, class I | −0.7(a) |
| Trucking, except local | 2.9(a) |
| Trucking, except local, general freight | 3.4(a) |
| Air transportation | 2.7(b) |
| Petroleum pipelines | 0.3 |
| Utilities | |
| Telephone communications | 5.8 |
| Gas and electric utilities | 0.5 |
| Electric utilities | 1.4 |
| Gas utilities | −2.2 |
| Trade | |
| Scrap and waste materials | 2.2(c) |
| Hardware stores | 1.3 |
| Department stores | 2.6 |
| Variety stores | −0.2 |
| Food stores | −0.8 |
| Grocery stores | −0.8 |
| Retail bakeries | −1.7 |
| New and used car dealers | 1.2 |
| Auto and home supply stores | 2.8 |
| Gasoline service stations | 3.1 |
| Apparel and accessory stores | 2.5 |
| Men's and boys' clothing stores | 1.2 |
| Women's clothing stores | 3.8 |
| Family clothing stores | 1.8 |
| Shoe stores | 1.6 |
| Home furniture, furnishings, and equipment stores | 3.4 |
| Furniture and home furnishings stores | 1.6 |
| Appliance, radio, TV and computer stores | 5.9 |
| Household appliances stores | 4.2 |
| Radio, television and computer stores | 6.2 |
| Eating and drinking places | −0.3 |
| Drug stores and proprietary stores | 0.9 |
| Liquor stores | 1.0 |
| Services | |
| Commercial banks | 2.0 |
| Hotels and motels | −0.3 |
| Laundry, cleaning, and garment services | −0.9 |
| Beauty and barber shops | 0.5 |
| Beauty shops | 0.1 |
| Automotive repair shops | −0.3 |
| Notes: (a) 1973 to 1989. (b) 1973 to 1991. (c) 1977 to 1992. |
|
Most of the BLS indices in Table 5 refer to retail trade. While the array of growth rates may appear to be highly heterogeneous, there is a distinct pattern.
Retail establishments involved with food and drink have a poor productivity record. These include food and grocery stores, retail bakeries, and eating and drinking places. Most other types of retailing have respectable to excellent productivity growth rates, with the best records recorded for stores selling consumer durables like television sets and appliances.
The BLS data record the same dismal record for services as do the NIPA, except for commercial banks. Here the difference has a simple source – the NIPA make no attempt to measure productivity for banking and simply set output growth equal to the growth in input, thus assuming productivity growth of zero by definition. In contrast, the BLS makes an attempt to measure the volume of transactions for three types of banking activity: deposits, loans and trusts.
2.4 Summary of the Evidence
The productivity performance of the American economy is poor on average, but highly heterogenous at the detailed industry level. This suggests that the search for explanations must examine aspects of particular industries rather than searching for one or two general, overarching explanations. There are a surprising number of industries that are star performers, with productivity growth rates above 4 per cent for the 1979–92 period (in Table 4). These include farming, metal and coal mining, industrial machinery, electronic equipment, instruments, leather products, railroads, and telecommunications. But, as an offset, there were other industries with negative productivity growth over the same period, including printing and publishing, tobacco manufactures, pipelines, real estate, and within the services sector, business, auto repair, health, legal, and miscellaneous services.
3. A Litany of Measurement Issues
A number of measurement problems taint the legitimacy of comparisons of productivity performance across time, across industries, and across countries. This section provides an introduction to the general class of measurement issues that relates to productivity performance, particularly in the services sector. Then more detailed sections follow that highlight the major issues relevant to cross-time, cross-industry, and cross-country comparisons.
3.1 Interrelation Among Measurement Issues
Since the post-1973 productivity-growth slowdown has eluded a convincing and general explanation, an appealing goal for research would be to identify a set of measurement problems that could fully explain the slowdown. However, this is unlikely to occur, for two basic reasons. First, to contribute any explanation of the overall US productivity slowdown, a given measurement problem must have caused aggregate output growth to have been understated more (or aggregate input growth overstated more) after 1973 than before. Some of the most important types of measurement error, particularly those involving a failure to adjust price deflators adequately for quality change, may have been as important or even more important before 1973.
Second, it is not enough to demonstrate that there is a measurement problem at the industry level, because the output of many industries (e.g. railroad freight) consists of intermediate goods. An understatement of output growth in an intermediate sector results in an understatement of input growth in the sector producing final output using intermediate inputs. Thus, a demonstration that a measurement problem biases the output growth of a particular intermediate industry just reshuffles productivity growth among industries without explaining the aggregate slowdown. For instance, an understatement of output growth in the railroad freight industry would be a pure industry phenomenon, since all of railroad freight output is an intermediate good. But an understatement of real consumer purchases of air transportation would contaminate both productivity growth in the airline industry and in the economy as a whole. Many of the debates in productivity measurement concern the validity of industry measures and imply more for the industry allocation of productivity growth than for the overall magnitude of the slowdown.
To summarise this point is to establish four quadrants on a simple grid as a classification of actual or possible measurement errors.
| Affects aggregate economy, contributes to post-1973 slowdown. | Affects aggregate economy, but same effect pre and post 1973. |
|---|---|
| Contributes to post-1973 slowdown for an industry, no aggregate impact. | Measurements error that applies pre and post 1973, no aggregate impact. |
Only measurement issues that qualify for the north-west corner of this quadrant help to explain the productivity growth slowdown. Issues relating to the south-west corner are those that reshuffle the industry allocation of productivity change. Issues entering the quadrants in the eastern half of the table could create a secular bias in productivity at the aggregate (north-east) or industry (south-east) levels, but have no implications for the slowdown.
However, from an international perspective, the north-west quadrant is not the only interesting aspect of measurement issues. Identification of measurement errors that ‘reshuffle’ the industry distribution of productivity growth may change the distribution of growth rates across industries and countries. A particular substantive explanation may gain or lose plausibility if attention to measurement issues creates convergence or divergence of a particular industry viewed across countries. Similarly, measurement errors in the north-east or south-east corners of the grid that apply both before and after 1973 may still be interesting to learn about. A sufficient upward bias in the price deflator for consumer goods in the United States, for instance, could imply that real wages have grown substantially since 1973 rather than stagnating. This would be important news, even if the same error implied that growth in productivity and real wages prior to 1973 had been understated as well.
With improved methodology and larger budgets, how could measurement methods have deteriorated since 1973? Is that not a prima facie argument against measurement errors as a cause of the productivity slowdown? The primary reason to suspect that there may have been a measurement-related component to the slowdown is not that the official statistical agencies have become worse, but rather than the economy has become harder to measure. According to ball-park estimates by Griliches (1994, p. 11), the fraction of the American economy consisting of sectors with output that is ‘hard to measure’ has increased from 51 per cent in 1947 to 69 per cent in 1990.
This review of measurement problems begins with two general sets of issues that are not confined exclusively to the service sector – that is, weighting problems (particularly aggravated in the US through the influence of the hedonic deflator for computers and a single base-year weighting scheme) and sources of bias in the basic source of price data used in deflating most of the output of final goods and services, namely the US CPI. We shall then turn to specific problems that affect the validity of measurement of output and productivity in the US service sector.
3.2 Index Numbers and Additivity
The most important point about weighting schemes and index numbers is that weights should change frequently. There is a class of index numbers that Diewert (1987) has classified as ‘superlative’ which allow weights to change frequently but differ in minor ways, depending on the duration of the period over which weights are averaged, and how the averaging is carried out. These desirable index numbers, often referred to as ‘Fisher-ideal’ or ‘chain-weighted’ index numbers, represent a theoretical ideal that is far from the practice of the US NIPA.[2]
The US NIPA are quite unique, in comparison with other countries, in their steadfast insistence on a single base year that applies to all calculations of real variables – that is, real GDP, real consumption, real investment, and so on, from the dawn of the data through to the present. This leads to fallacious indices that are widely used and analysed, and yet which the producers of the data (the Bureau of Economic Analysis, or BEA) know are misleading and, for some purposes, lead to the opposite conclusions of the truth.
First, let us review the simple logic behind the error of using a single base year, and then examine some of the consequences. The official US measure of real GDP in 1987 weights sub-components of output by their relative prices in 1987. To focus on the effect, consider the different impact of government expenditures, which have an increasing relative price over the decades, and of producers' durable equipment, in which there is an important component of computing equipment, which has a (rapidly) declining relative price over the decades.
Consider first the years prior to 1987, when government expenditures were relatively cheaper than in 1987. The official 1987 weights based on 1987 relative prices will overweight government expenditures for years prior to 1987 and will underweight government expenditures for years after 1987. Since government expenditures always increase in wartime, the relative size of government (and of World War I or World War II wartime expenditures) is much larger using 1987 as a base year than, say, 1944 or 1917. Further, the size of the exaggeration of wartime expenditures is not fixed, since the base year is regularly moved to a later date, e.g. from 1972 to 1982 to 1987. To dramatise the importance of this error in weighting procedures, l have often said ‘that every time the BEA moves the base year to a future year, World War I gets bigger’.
Similarly, the 1987 base year procedure understates the importance of computers and other high-tech equipment prior to 1987. Since these have rapidly declining relative prices, prior to 1987 any component of GDP that includes computers is understated as a share of GDP, and the growth rate of GDP itself is understated. Everything is reversed after 1987. The relative size of government (or any other sector with a rising relative price) is understated. The relative size of computer investment, or any aggregate (like producers' durable equipment (PDE) or manufacturing output) that includes computer output, is overstated.
But the size of relative shares is a small part of the overall problem. Anyone who wants to check the movement of true shares is free to use nominal magnitudes. Instead, the real damage is done to measures of the growth rate of real magnitudes, essential ingredients in measures of productivity and our standard of living. Oddly, while the BEA publishes both fixed 1987 base-year measures of real output magnitudes and superior magnitudes based on chain-weighting and benchmark-weighting, almost no-one pays any attention to the superior measures.[3] Yet everyone, following Diewert (1987, 1995), agrees that they dominate the conventional fixed 1987-base-year measures, so much so that the latter are invalid measures of economic performance.
Does this make any difference? Table 7 shows that important conclusions about the true behaviour of the economy can be reversed when the official fixed 1987-base-year data are used in place of the theoretically preferable chain-weighted or benchmark-weighted indices. To understand this table, note that the columns display annual rates of growth over four periods, 1972–87, 1987–90, 1990–94 and 1987–94. That is, column (4) does not provide new information but rather provides a weighted average of the information in columns (2) and (3). Much of the following will be based on a comparison of the growth rates in columns (1) and (4).
| 1972–87 | 1987–90 | 1990–94 | 1987–94 | |
|---|---|---|---|---|
| (1) | (2) | (3) | (4) | |
| Real GDP | ||||
| Fixed 1987 weights | 2.75 | 2.68 | 2.00 | 2.29 |
| Chain-type weights | 3.03 | 2.70 | 1.72 | 2.14 |
| Benchmark weights | 3.10 | 2.68 | 1.74 | 2.14 |
| Real consumption of durable goods | ||||
| Fixed 1987 weights | 4.69 | 2.48 | 3.92 | 3.30 |
| Chain-type weights | 5.05 | 2.45 | 3.30 | 2.94 |
| Benchmark weights | 5.09 | 2.45 | 3.34 | 2.96 |
| Producers durable equipment | ||||
| Fixed 1987 weights | 4.69 | 3.25 | 7.90 | 5.91 |
| Chain-type weights | 5.79 | 3.18 | 6.00 | 4.79 |
| Benchmark weights | 6.69 | 3.45 | 6.20 | 5.02 |
| Non-farm private output per hour | ||||
| Fixed 1987 weights | 0.95 | 0.15 | 1.94 | 1.17 |
| Chain-type weights | 1.23 | 0.17 | 1.66 | 1.02 |
| Benchmark weights | 1.30 | 0.15 | 1.68 | 1.02 |
|
Note: Chain and benchmark versions of output per hour calculated by applying the differences for real GDP in the first three lines of the table. Sources: GDP, Consumption, PDE from Survey of Current Business, various issues; Output per hour from Economic Report of the President and Economic Indicators, various issues. |
||||
The lines of the tables appear in four sections representing real GDP, real durable goods consumption, producers durable equipment, and non-farm private output per hour. In every case, the theoretically predicted difference appears between the indices based on fixed 1987 weights, and the indices based on chain-type weights or on benchmark weights. That is, the fixed-1987-weight measures understate the growth rate of real magnitudes prior to 1987 and overstate them after 1987.
For two key issues the change in weighting schemes, from the unsatisfactory BEA scheme based on fixed (1987) prices to one of the moving-weight schemes favoured by Diewert, makes enough difference so that conclusions are reversed. Let's start at the bottom of Table 1, where data on the growth rates of productivity, measured as US non-farm output per hour are displayed. Comparing column (1) and column (4), we reach the conclusion – associated with such optimistic business economists as Stephen Roach of Morgan Stanley – that productivity growth has accelerated. Fixed 1987 weights indicate that between 1972–87 and 1987–94 productivity growth accelerated from 0.95 per cent per year to 1.17 per cent per year.
However, this conclusion turns out to be quite decisively wrong when recalculated with either chain-type weights or benchmark weights. Comparing 1972–87 versus 1987–94, chain-type weights indicate a productivity deceleration from 1.23 to 1.02 per cent per year. In other words, the correct moving-weight index indicates a productivity slowdown of the same order of magnitude as the incorrect fixed-weight index indicates a productivity acceleration. The difference is even greater for PDE, where the fixed-weight (official) indices indicates an acceleration from 4.69 to 5.91 per cent per year, while chain-type weights indicate a deceleration from 5.79 to 4.79 per cent per year. The difference between one measure and the other amounts to 2.2 per cent per year, a big deal when compounded out over 10 or 15 years.
Why has the BEA maintained the single-base-year approach for so long? As Diewert (1995) points out, there is a fatal theoretical contradiction between shifting weights and ‘additivity’. Simply put, if we shift weights every quarter, then the sum of the components of real GDP will not add up to total real GDP for more than a single quarter. The obvious retort to the ‘additivity’ dilemma is, ‘who cares?’. For any question involving shares of one component in the total economy, or a sub-component in a major part of the economy, the correct answer comes from shares of nominal (current dollar) spending or income, not real (constant dollar) income.
There is no additivity problem in nominal magnitudes and thus no problem in discussing shares of any component within any other component.
Perhaps we could agree that there is a ‘dichotomy’ in the use of national income statistics. Some people are interested in the cross-sectional relationships, i.e. relative magnitudes. For this nominal magnitudes are the correct measure. More often, we are interested in growth rates of real magnitudes, such as productivity growth (which in turn is the growth rate of output minus the growth rate of hours of labour input). Here we want the growth rates to be based on moving weights, a Fisher-ideal, Tornqvist, or chain-weighted measure. For growth rates, additivity does not matter.
Not only is the additivity dilemma irrelevant for nominal magnitudes but it is meaningless for real magnitudes. If we want the share of consumption in total real GDP (consisting of components C+I+G), we can measure that as C/(C+I+G). It is irrelevant whether the level total real GDP computed with a chain-weighted procedure differs from the total of C+I+G. Besides, with rapidly changing weights, shares in real GDP are unlikely to differ appreciably from shares in nominal GDP. Again, additivity does not matter.
3.3 Sources of Bias in Aggregate Price Indices
What matters for output and productivity growth is bias in the GDP deflator, not the CPI. Yet it is conceivable that the biases in the GDP deflator and CPI could go in the opposite direction, because of the base-year bias discussed above. Real GDP growth is biased upward after 1987 because of the use of fixed 1987 weights rather than a moving weight system like chain-weighting or benchmark weights. Yet the CPI is widely believed to be biased upward throughout the post-war period. This issue, for which no one has yet provided quantitative measures that balance the opposing sources of error, implies that the direction of bias in aggregate measures of output after 1987 is uncertain, since weighting bias that raises the growth rates of real magnitudes is/may be overwhelmed by CPI bias that reduces the growth rates of real magnitudes. Obviously, before 1987 both sources of bias work in the same direction and imply that the growth rate of real GDP and of productivity is understated. This is not good news for those attempting to explain the productivity-growth slowdown.
Why are we now quite certain that the CPI incorporates a substantial upward bias? There are at least four reasons.
1. Traditional Substitution Bias. The CPI is what is known as a ‘Laspeyres’ price index. That is, it measures price changes for many different products and then aggregates these thousands of separate measures of price change using weights that apply to a base year (or years) that is prior to the period being measured. Over much of the post-war period, these weights in the CPI have been based on consumer expenditures from five to fifteen years prior to the year of price measurement. In the traditional example, even if the price of chicken rises much less than the price of beef so that consumers shift their expenditures to chicken, the relative weight of chicken and beef in the CPI is based not on current spending patterns but rather on expenditures in that long-ago base year. Economists used to study this traditional substitution bias quite a lot, until they found out that it didn't amount to much. The consensus estimate for this first source of bias is 0.25 per cent per year.
2. Quality Change. It is widely recognised that the CPI fails to adjust adequately for the improved quality of new products and new models. To set this problem in context, students of business history have drawn attention to the ‘product cycle.’ New products – whether autos, air conditioners, or VCRs – are initially made in small volumes and sold at high prices. Soon, firms figure out how to increase volumes and reduce prices. Eventually products mature, sales fall off, and prices increase more rapidly than the average product. The sequence is easily visualised as a U-shaped curve – the price of any given product relative to the consumer market basket starts high, then goes down, is flat for a while, and then goes back up.
Nobody debates the reality of this product cycle, and nobody debates the fact that the CPI introduces products late, thus missing much of the price decline that typically happens in the first phase of the product cycle. This is the first aspect of quality change bias. For example room air conditioners were widely sold in 1951, available in the Sears catalogue and rated by Consumer Reports in 1952, but not introduced into the CPI until 1964, 12 years late! More recently, the microwave oven, VCR, and personal computer were all introduced into the CPI years after they were sold in the marketplace. In short, the CPI introduces new products too late and tracks obsolete products too long.
The second aspect of quality change bias results from a narrow definition of a commodity. Before 1970 precise multiplication and division required noisy and expensive rotary electric calculators; after 1970 electronic pocket calculators became available and are now in the pocket or dormitory of every college student. The price fell quickly from $1,000 to $10, and the new product could do exponents, logarithms, and lots of things the old product could not do. But the price decline was completely ignored by the government price indices, which treated the old and new calculators as separate products. People flock to rent videos but the declining price of seeing a movie at home, as compared to going out to a theatre, is entirely missed in the CPI. Similarly, the CPI misses the replacement of manual typewriters by electronic typewriters and then PCs with word-processing capability.
The third aspect of quality change bias results from a narrow definition of quality. Newly-improved models are often introduced with new features that are missed by the CPI. Changes occur in energy efficiency and repair frequency, but these are rarely if ever valued in compiling the CPI. Here is a brief list of some of the quality improvements that have been ‘missed’ by the CPI over the post-war years:[4]
- improved ability of refrigerator-freezers to hold a zero temperature;
- reduced electricity consumption of all appliances, particularly refrigerators and TV sets;
- reduced repair costs on TV sets and indeed all appliances;
- reduced vibration, noise, and discomfort in air travel as jets replaced piston planes and as air travel became safer;
- the enormous improvements in the audio quality of home and auto stereo equipment;
- the shift from metal to plastic that reduced corrosion and increased lifetimes for so many consumer products;
- the reduced weight of home power tools;
- the reduction of noise, weight, bulk, and installation cost of room air conditioners; and, to bring home the point to almost everyone in this room; and
- the immeasurable increase in picture quality of colour TV sets compared to the dim, flickering images of the mid 1960s.
How much does this second source of CPI bias amount to? For some products it is very large – 6 per cent per year for the radio-TV category over the 37 years studied in my book (Gordon 1990). For other products, it is much less. I estimated that for consumer durables the upward bias was 1.5 per cent per year for the post-war period, assuming that the half of consumer durables that I didn't study were measured perfectly (it is likely that an inquiry into that other half would turn up additional bias). Even in such traditional products as apparel, there seems to be a substantial bias – in recent unpublished historical research I have identified a 2.1 per cent per year upward bias in the CPI for apparel between 1920 and 1947. If the only quality bias was in the durables I measured in my book, the implied bias for the total CPI would be 0.3 per cent per year. Adding in plausible bias in non-durables and services (including medical care), we could easily double that to, say, 0.6 per cent per year.
3. Outlet Substitution Bias. Just as the CPI has a narrow definition of a product, it has a narrow definition of where a product is sold. A banana is not a banana. If a pound of bananas initially costs $0.69 at Ace supermarket, and ‘Ultra Discount Superstores’ comes to town and starts selling bananas for $0.49 per pound, the consumer enjoys a price decline of 29 per cent. But the CPI registers a price decline of zero! Why? Each outlet is assumed to provide a separate set of services. But consumers have been leaving ma-and-pa drug stores in droves to shop at Walmart, ma-and-pa toy stores to shop at Toys ‘R’ Us, and ma-and-pa hardware stores to shop at Home Depot. So we know that individual consumers have enjoyed a price decline that is not measured at all in the CPI.
A related source of bias is that the US government price indices for drugs treat brand-name and generic drugs as separate commodities. Thus when the market shifts from brand-names to generics (which generally are introduced at about half the price), the price index does not fall while measured revenue does fall, leading to a spurious decline in output and productivity in the pharmaceutical industry.
4. The Logarithm Bias. The most embarrassing source of bias in the CPI was brought to light by the BLS itself. To put it bluntly, the CPI doesn't understand logarithms. Using the methodology of the CPI, if a piece of apparel goes on sale from $100 to $75, that represents a price decline of 25 per cent. When the item goes back to the regular price of $100, that represents a price increase of 33 per cent. True change in price from beginning to end? Zero, the answer that would be obtained by using logs. The CPI measured change in price? Plus 8 per cent! Careful BLS research has shown that this contributes a bias of about 2 per cent per year for produce and female apparel in a recent period, and a bias for the total CPI of about 0.35 per cent per year.
3.4 Implications for Productivity Growth
The set of CPI measurement bias sources outlined above is by far the largest part of the productivity measurement story. Recall from our four-quadrant matrix that a particular source of measurement bias must apply to purchases of final goods and services in order to imply an alteration to official productivity growth measures for the aggregate economy (in contrast to a bias applying to intermediate goods and services that merely reallocate productivity growth among sectors). By definition, the CPI applies to final purchases of consumer goods and services, and so any bias identified in the CPI directly implies a bias in the opposite direction in measures of productivity for industries producing consumer goods and services.
Where do the individual sources of CPI bias alter the record of productivity growth recorded in Tables 1 to 5? Traditional substitution bias and outlet substitution bias imply that actual productivity growth has been more rapid than officially recorded in manufacturing and trade. Quality change bias applies in many consumer purchase sectors, from durable goods like VCRs and microwave ovens to services like banking, insurance, and health care. Finally, the ‘logarithm’ bias creates a substantial overstatement of price increases for produce and apparel, implying an understatement of productivity growth in the apparel part of manufacturing and in retail trade.
3.5 Additional Sources of CPI Bias
Even the radical estimate presented here of the CPI bias is surely an understatement of the true bias, for new products raise the standard of living in ways that go far beyond simple price changes for a single product. The price of light was reduced enormously by the invention of electricity, but until recent pioneering work by Nordhaus (1995) there was no price index that directly compared the price per lumen of a primitive 1890's electric light bulb with that for a whale-oil lamp. And even such an adventuresome price index makes no attempt to measure the value to families of extending day into night, or for firms in being able to extend the hours of production from a given set of facilities.
Whatever invention we take – whether the automobile that allowed limitless flexibility in the time and destination of rapid transportation, or the jet plane and communications satellites that tied together far-flung nations into a single international community, or the television and VCR that allowed almost any motion picture to enter the home, or the new-fangled PC with CD-ROM that promises ultimately to bring the Library of Congress into every home – these new developments have made human life better on a large scale.
The ultimate test of the change in the cost of living over the past 25 years is to ask the following question. Take the market basket of goods and services available in 1970 and labelled with 1970 prices. Take the market basket available in 1995 and labelled with today's prices. Ask the consumer, how much more income would you require to be as satisfied with the 1995 basket and prices as with the 1970 basket and prices? The CPI says 4 times as much income would be necessary, because the CPI has quadrupled since 1970. But that 1970 market basket has no VCRs, microwave ovens, or computer games; its colour TV sets break down all the time; and its refrigerators use a lot of electricity. Consumers forced to answer my question are going to miss all the benefits of modern life and are not going to say that four times as much income would be necessary – maybe 3 times, maybe 2 times, but not 4 times. That's the ultimate test of bias in the CPI. Note that if the correct answer is ‘3 times,’ the bias in the CPI has been running at an annual rate of 1.2 per cent, while if the correct answer is ‘2 times,’ the bias instead is 2.8 per cent.
4. Measurement Problems at the Industry Level in an International Context
In addition to the set of measurement issues outlined above, there are others related to specific industries. It helps to understand some of the issues involving particular industries if we compare measurement methods in the US with several other large countries, particularly France, Germany and the UK.
At the general level of output and price measurement, we stress one area in which US methods seem inferior to those used in the other countries – weighting methods. As we have seen above, the United States uses a single base year (which other countries like France, Germany, and the UK avoid through frequent changes in weights), and the compounding of the error of using a single base year through the introduction of a hedonic price index for computers that creates huge changes in relative prices within particular sectors of the aggregate economy, particularly durable manufacturing.
The US is apparently the only country that forces the relative price of a single base year to apply throughout the history of the national accounts, although an alternative chain-weighted index of GDP and its major components is now published for the period since 1959. The use of shifting base years in France, Germany and the UK increases the accuracy of the relative price structure used to aggregate the output and price indices. This major advantage comes at a cost for users of the accounts: different sets of tables are provided for each base year, and the user must go to the extra work of linking when a long time series is desired. For instance, the French accounts are published for 1949–59 on a 1956 base, 1959–79 on a 1970 base, and 1970-present on a 1980 base. The need for linking extends to nominal series, not just real series, since new measurement methods are generally introduced as part of a new weighting system. Thus the nominal value of construction output in France for 1970 is different in the 1980-base accounts than in the 1970-base accounts. As the base year is updated, numerous other aspects of the accounts change, again inhibiting links. For instance, the French accounts are available at a progressively greater level of industry detail as the base year shifts from 1956 to 1970 to 1980.
The German system is similar to the French in most respects. The UK accounts rebase every five years. Historical UK data for 1978–83 use 1980 weights, 1983 to 1988 use 1985 weights, and so on. Frequent UK rebasing carries with it a cost in terms of ease of data availability; we are informed, for instance, that the UK producer price statistics are simply not available for l980 in a product breakdown comparable to the pre-1980 period.
4.1 Specific Industries
I have identified several industries in which US measurement methods differ from those used in other major nations.
Transportation. The apparently uniform reliance of France and Germany on double deflation conceals important differences across industries. Double deflation means that an attempt is made to subtract the real value of materials inputs, deflated separately. But this does not mean that gross output is obtained in all cases by the use of detailed price indices as deflators. Instead, in Germany and France, volume indicators are used in some industries. An example is rail transportation in Germany, where ton-mile indices are developed for 100 different categories of freight and aggregated using base-year value-per-ton-km weights; the substantial data requirements of this method are facilitated by the monopoly position of the Deutsche Bundesbahn. The method is similar in principle that is used in the US by the BLS productivity program (as summarised above in Table 5) to measure gross output. However, the German method is more detailed in application, adjusts for materials outputs, and presents a unified story for the different forms of transportation, in contrast to the US, where the national accounts indicate substantially slower output growth than the BLS. Interestingly, the only fact about the French treatment of transportation that we have digested so far is that the French CPI, intended to provide price information for urban workers, covers only the packaged tour component of air transportation.
Real Estate. Both France and Germany deflate gross output with rental price indices, as in the US. The US rental price indices are sometimes accused of a downward bias by tracking a progressively older rental housing stock and failing to correct for the declining quality that, some allege, comes with increasing age. However, maintenance and remodelling may actually lead to an improvement in quality. The fraction of the rental housing stock equipped with central air conditioning, built-in appliances, etc., has increased alongside the fraction of the owner-occupied housing stock displaying these additional quality attributes.
In both Germany and France a substantial effort is made to correct the rental price
indices for quality change. In Germany new buildings are folded into the sample
regularly; presently the index is based on ten quality categories of apartments.
The French go further with a large sample of apartments stratified into 3,000
size/quality categories (square metres, presence of central heat, number of
showers/bathrooms, etc.). In France 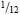 of the sample of apartments is replaced each
year. Comparisons of relative prices across countries are clouded by the different
importance of rent controls; presently about 30 per cent of French apartments
are rent-controlled.
of the sample of apartments is replaced each
year. Comparisons of relative prices across countries are clouded by the different
importance of rent controls; presently about 30 per cent of French apartments
are rent-controlled.
Insurance. Baily and I (1988) complained that productivity growth in the US insurance industry was understated due to an upward bias in the price indices used for deflation. Instead of measuring the price of what the insurance industry actually does, e.g. write policies, the US accounts use the prices of the activity being insured, mainly auto repair and medical care, and both of these exhibit substantial increases in relative prices. This problem is avoided in France, where gross output is measured not by deflation but by a physical volume measure (note in Table 5 above that the BLS does not provide a productivity index for insurance, even though in principle one could be created from an output measure based on the number of policies written and claims filed). In France, not only is the number of policies counted by standard categories of insurance, but the number of ‘elemental movements’ is processed on these standard categories. The current system contains 11 classes of ‘movements’ through 11 basic categories of policies. The system allows the monitoring of both the change in the stock of policies and the change in the numbers of policies issued in each category.
For insurance the German system relies more on deflation and less on the construction of volume indices. Nominal claims paid are deflated by different price indices – ‘special items’ from the CPI tor health insurance, the general consumption deflator for life insurance, and a special price index for auto repairs for casualty insurance. Thus it would appear that, in a world in which computers raise the ability of insurance employees to issue additional policies per employee, the French methodology would be more likely to capture the effects of the computer revolution than the German methodology.
Banking and Finance. The US industry data for banking and finance extrapolate output with labour input and assume no productivity change.[5] The French take the nominal production of the banking sector to be based on interest earned minus interest paid (for 80 per cent of bank output, volume indices for specific services for the other 20 per cent), deflated by a weighted average price index of bank services, including service charges on checking and saving accounts as well as credit card fees. The German approach is similar, taking gross nominal output to be the sum of sales from goods, commissions, and fees, plus interest received, less interest paid. Then consumption of intermediate goods, consumption of fixed capital, and taxes linked to production are subtracted, to arrive at net value added at factor cost. Unlike the French procedure which uses prices of explicit bank services, the Germans deflate net value added obtained in this way by the aggregate price index of national expenditure, at least for banks. For other credit institutions they rely on a price index for service charges in the CPI.
4.2 Implications of Differences in Measurement Methods
There are a number of differences in measurement methods between the US and several other major industrial nations. There are enough measurement issues to suggest that the unique American discrepancy between buoyant post-1979 productivity growth in manufacturing and near-total stagnation outside of manufacturing is partly spurious. In European nations the growth rates of manufacturing and non-manufacturing productivity are much closer together, and the true rates for the US manufacturing and non-manufacturing sectors are probably closer together also.
5. Hypotheses to Explain the Productivity Slowdown
As we have seen, the US economy has not experienced a uniform slowdown in productivity growth across all industries. The problems are concentrated in particular sectors. Thus a simple way of evaluating alternative hypotheses is to ask whether they shed light on cross-industry differences in productivity performance.
5.1 Measurement
Measurement problems related to specific industries, particularly finance, insurance, and real estate, have been reviewed above. The various sources of CPI bias suggest that productivity growth has been understated in manufacturing, retail trade, and some services. While most of these measurement problems were present long before the advent of the post-1973 productivity growth slowdown, we must recognise, as Griliches (1994) emphasises, that economic activity has shifted toward sectors in which output is intrinsically hard to measure. In his dichotomy, the economy is divided into two types of sectors, ‘measurable’ and ‘hard-to-measure’.
One weakness of the Griliches ‘hard-to-measure’ hypothesis is that it should apply equally to all nations, whereas Table 8 reports that productivity growth in the hard-to-measure sectors tend to be substantially more rapid in Japan and Europe then in the US. As we have seen, part of this difference, particularly in the finance, insurance and real estate sector, may be attributed to measurement issues. A large question originally asked by Baily and myself (1988) and more recently reviewed by Griliches (1994) is why a vast investment in computers has, at least in the US, produced so little payoff in productivity growth? Griliches shows that three-quarters of this computer investment has gone into the hard-to-measure sectors. Visible payoffs from computer investment, like rapidly rising volumes on securities and commodities exchanges, and the convenience of 24-hour banking with automatic teller machines, are largely missed in the productivity data.
| Measurable | Share of GDP in 1990 % |
Hard-to-measure | Share of GDP in 1990 % |
|---|---|---|---|
| Agriculture | 2.0 | Construction | 4.4 |
| Mining | 1.8 | Wholesale trade | 6.5 |
| Manufacturing | 18.4 | Retail trade | 9.3 |
| Transportation | 4.7 | Finance, insurance and real estate | 17.7 |
| Utilities | 4.0 | Other services | 18.9 |
| Government | 12.2 |
5.2 Standard Suspects
So much has been written about standard hypotheses to explain the productivity growth slowdown that we can mention them very briefly here. The inadequate US saving rate is indeed part of the problem, and that is evident in Table 1, where the slowdown in MFP growth in non-manufacturing is two-thirds of the slowdown in output per hour growth. Nevertheless, this still leaves a MFP slowdown of one per cent calling out for an explanation.
A separate aspect of inadequate investment is an alleged deterioration in infrastructure, i.e. public capital. In view of the lavish investment of the United States in interstate highways, cloverleafs, and posh airline terminals serving even medium and small-sized communities, this hypothesis seems dubious. A careful cross-country examination by Ford and Poret (1991) revealed no convincing evidence of a role for infrastructure in explaining cross-country differences in productivity performance.
The timing of the slowdown originally cast the oil price shocks of the 1970s as prime culprits, but this explanation has long since lost its credibility as the real price of oil has returned close to its pre-1973 values. Also, the cross-industry pattern of the slowdown does not lend credence to the oil price hypothesis, as such energy-intensive industries as airlines and utilities do not reveal a slowdown in the 1972–87 period followed by a compensatory revival.
A plausible culprit capable of explaining part of the slowdown is a decline in labour quality. The percentage of teenagers and adult women in the labour force rose after 1973, yet their average wages still lag behind those of adult men. Whether this represents a decline in labour quality is debatable, depending on how much of the wage difference reflects true differences in productivity, and how much represents discrimination. Baily and I (1988) suggested that about 0.3 percentage points of the slowdown might be attributed to some combination of the mix shift in labour compositions, and the decline in standardised test scores over the past two decades.
5.3 Two Plausible Explanations
My favourite list of explanations of the productivity growth slowdown include, of course, the measurement issues emphasised above, particularly in construction, finance, insurance and real estate and those sectors influenced by the CPI bias. However, there remain problem industries where measurement is not a suspect. In electric utilities and air transportation, the productivity growth slowdown is real and has a simple explanation – technological depletion or, more simply, ‘running out of ideas’. In both industries, based on the technology of large turbines, a frontier of size, speed, and pressure was reached and is unlikely to be surpassed. Poor productivity growth in US food retailing may also have a depletion aspect: ‘they could only invent the supermarket once’.
In addition to measurement and depletion, my other favourite explanation of the particular US pattern of the slowdown is that a structural shift in the operation of the US labour market has reduced real wages in the bottom half of the income distribution, and this has fed back into lower productivity (or slower growth). Simply put, the labour supply curve has shifted out, sliding down the labour demand curve. The sources of the structural shift are weak unions, a decline in the share of employment in industries where unions are strong, a substantial decline in the real minimum wage, and substantial immigration, both legal and illegal. This hypothesis is explored at length in Gordon (1995), but its role in explaining slow productivity growth in retail trade and services is evident from casual observation. US restaurants, particularly at the medium and higher price range, tend to have more serving personnel and layers of servers than their counterparts in Europe (it is standard in Chicago to have one layer taking orders, another delivering food from the kitchen, and a third (‘bus boys’) setting and clearing tables). In the US, at least everywhere I look, it is commonplace to have two people at each supermarket checkout lane, one tallying up the bill and the other ‘bagging’ each customer's order. Automated parking lots, with machines instead of cashiers, are more common in places like Sweden than in the US.
6. Conclusion
I have previously called attention to a dichotomy in macroeconomics. European economists concentrate on explaining structural unemployment and understanding impediments to labour-market flexibility (Gordon 1995). American economists are concerned with slow growth in productivity and real wages, and growing inequality of the income distribution. Too little work is done on either side of the Atlantic (or Pacific) to understand differences across countries and industries in the growth of productivity, the basic source of economic progress.
This paper has identified a number of important differences between the productivity performance of the US and other leading industrial nations. US manufacturing productivity has not experienced a slowdown when 1972–94 is compared with 1950–72, but official data overstate the post-1987 growth of manufacturing productivity. Much of the post-1972 slowdown is concentrated in particular industries outside of manufacturing, and output in many of these industries is intrinsically hard to measure. A host of measurement problems suggests that US productivity growth is substantially understated, both before and after 1972, with the fraction of economic activity taking place in ‘hard-to-measure’ sectors suggesting a possible increase in the seriousness of measurement difficulties.
In addition to measurement problems (some but not all of which are similar in other countries), two substantive hypotheses are proposed to explain the productivity slowdown. First, technological depletion has played a role, particularly in electric utilities, air transportation, and food retailing. Second, the weak bargaining position of labour in the United States may have contributed to slow productivity growth, particularly in the services, by leading to low wages in the bottom and consequent overstaffing.
Footnotes
Sources of discrepancies between the NIPA and BLS are examined in detail in Gordon (1992, pp. 374–382). [1]
Those in charge of the NIPA are well aware of these problems and may be on the verge of changing to a superlative index number scheme for aggregate real GDP. [2]
The BEA's benchmark weighting system weights the growth rates of real sub-aggregates (e.g. real durable consumption) by the average of nominal expenditure shares in benchmark years five years apart, e.g. 1982 and 1987. [3]
This list is an excerpt from Gordon (1990, pp. 38–39). [4]
We note in Table 4 that the NIPA measure of output per person engaged in the industry ‘security and commodity brokers’ grows at a substantial rate after 1987, indicating a change in measurement methods. I have not yet been able to identify the nature of this change. [5]
References
Baily, M.N. and R.J. Gordon (1988), ‘The Productivity Slowdown, Measurement Issues, and the Explosion of Computer Power’, Brookings Papers on Economic Activity, 2, pp. 347–420.
Diewert, W.E. (1987), ‘Index Numbers’, in Eatwell et al. (eds), The New Palgrave: A Dictionary of Economics, Macmillan, London, pp. 767–780.
Diewert, W.E. (1995), ‘Price and Volume Measures in the System of National Accounts’, in J. Kendrick (ed.), The New System of National Economic Accounts, Kluwer Publishers, Norwell (forthcoming).
Ford, R. and P. Poret (1991), ‘Infrastructure and Private-Sector Productivity’, OECD Economic Studies, No. 17, pp. 63–89.
Gordon, R.J. (1990), The Measurement of Durable Goods Prices, University of Chicago Press, Chicago.
Gordon, R.J. (1992), ‘Productivity in the Transportation Sector,’ in Z. Griliches (ed.), Output Measurement in the Service Sectors, University of Chicago Press, Chicago, pp. 371–422.
Gordon, R.J. (1995), ‘Is There a Tradeoff Between Unemployment and Productivity Growth’, NBER Working Paper No. 5081.
Griliches, Z. (ed.) (1992), Output Measurement in the Service Sectors, Chicago, University of Chicago Press, Chicago.
Griliches, Z. (1994), ‘Productivity, R&D, and the Data Constraint’, American Economic Review, 84(1), pp. 1–20.
Nordhaus, W.D. (1995), ‘Do Real Output and Real Wage Measures Capture reality?’, The History of Lighting Suggests Not', in T. Bresnahan and R.J. Gordon (eds), The Economics of New Goods, University of Chicago Press, Chicago (forthcoming).