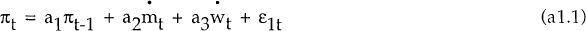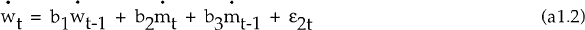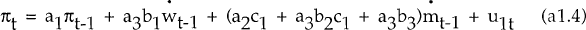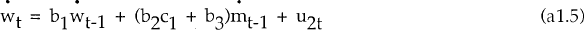RDP 9105: Inflation in Australia: Causes, Inertia and Policy Appendix 1: Granger Causality and Exogeneity

In this appendix we demonstrate that, under weak assumptions, Granger non-causality implies weak exogeneity. Consider the following structural model of inflation:

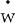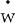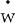where π is the rate of inflation, is the growth rate of money and is the growth rate of nominal wages. is weakly exogenous (with respect to the variables π and ). is weakly exogenous if b₂ = b₃ = 0. Conditional on this being true, 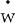is an exogenous determinant of π if a₃ ≠ 0, while is an exogenous determinant of π if a₂ ≠ 0.

The reduced form of this system is:

fails to Granger cause 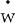if b₂c₁ + b₃ = 0. In itself, this does not imply anything about the exogeneity of 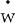. However, if we make the reasonable assumption that c₁ > 0, then b₂c₁ + b₃ = 0 implies b₂ = b₃ = 0 i.e. 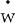is weakly exogenous.

does not Granger cause π if a₂c₁ + a₃b₂c₁ + a₃b₃ = 0. Again assuming c₁ > 0, and conditional on the weak exogeneity of 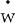, this implies a₂ = 0 i.e. is not an exogenous determinant of π. Finally, 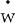Granger causes π if a₃b₁ ≠ 0. This implies a₃ ≠ 0 i.e. 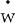is an exogenous determinant of π.

Thus, the combination of 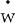Granger causing π, not Granger causing 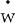or π, and the assumption of c₁ > 0 implies that 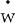is an exogenous, structural determinant of π but is not.

This demonstration can be easily extended to more complicated structural models.