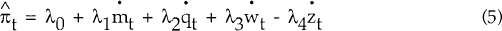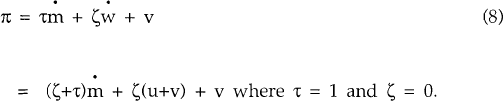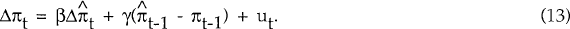RDP 9105: Inflation in Australia: Causes, Inertia and Policy 2. The Structural Model: Specification
July 1991
- Download the Paper 350KB
(i) The Equilibrium Inflation Rate
The equilibrium inflation rate is determined by the following three-equation structural model, with all the variables, except the nominal interest rate, i, specified as natural logarithms.
Equation (1) shows output, y, to decrease as the real interest rate increases and to increase as the real exchange rate depreciates. To abstract from nominal exchange rate effects, foreign prices, q, are measured in units of the domestic currency. Equation (2) is an equilibrium condition for the money market. Equation (3) is an aggregate supply function, with the price level p increasing with output and the nominal wage level, w, and decreasing with the level of (total factor) productivity, z.
These equations can be re-arranged to show that
| where | ψ1 = δ1α1/(θ2+α1θ1+δ1(α1θ2+α1+α2θ2)) |
| ψ2 = δ1θ2α1/(θ2+α1θ1+δ1(α1θ2+α1+α2θ2)) | |
| ψ3 = δ1θ2α2/(θ2+α1θ1+δ1(α1θ2+α1+α2θ2)) | |
| ψ4 = δ2(θ2+α1θ1)/(θ2+α1θ1+δ1(α1θ2+α1+α2θ2)) | |
| ψ5 = δ3(θ2+α1θ1)/(θ2+α1θ1+δ1(α1θ2+α1+α2θ2)) |
The expression for the equilibrium inflation rate,  , is derived by
noting that Etpt+1 = Etπt+1 + pt,
making the simplifying assumption that Etπt+1 = Et−1πt
and taking first differences of (4):
, is derived by
noting that Etpt+1 = Etπt+1 + pt,
making the simplifying assumption that Etπt+1 = Et−1πt
and taking first differences of (4):
| where | λ1 = ψ1/(1−ψ2) |
| λ2 = ψ3/(1−ψ2) | |
| λ3 = ψ4/(1−ψ2) | |
| λ4 = ψ5/(1−ψ2) |
and where · above a variable denotes a growth rate.
Since ψ2 < 1 the equilibrium inflation rate covaries positively with the growth rates of money, nominal wages and foreign prices and negatively with productivity growth. λ0 is a constant. Estimation of the parameters in (5) should yield the relative contributions of these variables to the equilibrium inflation rate.
In a recent review of the inflation literature, McCallum (1990) observes that there is little professional disagreement nowadays with Milton Friedman's dictum that “inflation is always and everywhere a monetary phenomenon” (1963 p17), provided that one abstracts from the effects on inflation of supply shocks, which are assumed to be temporary and of relatively small magnitude. Strictly speaking, however, the correct statement is that “inflation is a phenomenon of the economy's exogenous nominal variable”. This variable is assumed by quantity theorists (like Friedman) to be money since, in principle, it is under the control of the central bank. Given this assumption, the paths of all other nominal variables, including wages, are determined by the growth rate of the money supply.
The validity of this assumption is determined by the nature of the economy's wage-setting institutions, which will vary from country to country. For Australia, we believe that a reasonable case can be made that nominal wages are exogenous, in the sense that they are largely set by the political process (e.g. the present Prices and Incomes Accord). This does not mean that nominal wages will never be altered in response to changing economic circumstances, but it does mean there is no automatic tendency for nominal wage growth to follow changes in the growth rate of the money supply, as the quantity theorists would have us believe.
If nominal wage growth is determined exogenously, the question of interest is which of the growth rates of money and nominal wages gives superior information as to the likely present and future paths of price inflation. If, for example, the velocity of money is highly variable, the growth rate of the money supply will not be as good a predictor of price inflation as the growth rate of nominal wages. This will be particularly so if prices in the economy are set as markups over costs.
It needs to be emphasised that the exogeneity of money is not relevant here, and the seemingly endless debate about the exogeneity of money only serves to obfuscate the important issues.[3] It seems clear to us that, at least under floating exchange rates, the (narrowly defined) money supply is under the potential control of the central bank. However, the exogeneity of money in itself does not imply the existence of a simple correlation, much less causation, between its rate of growth and inflation of the price level.[4]
Clearly, these issues can only be resolved empirically. However, if the quantity theorists are correct, (5) is mis-specified since it assumes nominal wages growth to be exogenous and so least-squares estimation of (5) will lead to be biased and inconsistent estimates. This problem is unlikely to be serious, however, provided the growth rate of money dominates the growth of wages as a predictor of inflation. To see this, consider the following model of inflation which abstracts from the effects of productivity growth and foreign inflation.
(6) and (7) both follow from the assumptions of the quantity theory of money – up to the stochastic shocks u and v, the growth rates of real wages and the real money supply will be constant in long-run equilibrium.
Noting that (6) and (7) imply that 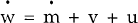 , the system can be written as
, the system can be written as
Since  is
exogenous,[5]
the OLS estimate
is
exogenous,[5]
the OLS estimate 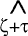 is unbiased.
is unbiased.
However, 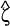 is biased since
is biased since
The extent of the bias depends on the ratio  . This ratio will be
small and so
. This ratio will be
small and so 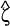 will be close (but not equal) to zero provided money
growth conveys significantly more information than nominal wage growth about inflation, which
will certainly be the case when
will be close (but not equal) to zero provided money
growth conveys significantly more information than nominal wage growth about inflation, which
will certainly be the case when  is exogenous and
is exogenous and 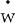 is
endogenous.
is
endogenous.
The case where both  and
and 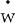 are exogenous
can be represented by the model
are exogenous
can be represented by the model
where z is a stochastic error term.
No simultaneity bias arises here; the question of interest is the relative size of  and
and 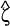 . This is
easily resolved by noting that
. This is
easily resolved by noting that
and
Clearly, if money growth does not signal much information about inflation (because of, say,
random shifts in velocity) the denominator of (11) will be much larger than the numerator, and
 will
approach zero. On the other hand, if the growth rate of nominal wages does not signal much
information about inflation (because, say, real wage growth is determined by supply shocks that
have a large variance) then the denominator of (12) will dominate the numerator, and
will
approach zero. On the other hand, if the growth rate of nominal wages does not signal much
information about inflation (because, say, real wage growth is determined by supply shocks that
have a large variance) then the denominator of (12) will dominate the numerator, and 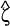 will tend
to zero.
will tend
to zero.
We conclude that a regression equation such as (5) will enable us to determine which variables convey the most information about the equilibrium inflation rate, irrespective of whether nominal wage growth is exogenous or endogenous.
(ii) Dynamics
The equilibrium inflation rate is that which is determined by long-term fundamentals. In the short-term, however, the presence of imperfectly competitive goods and factor markets – and hence price rigidity – implies that shocks to demand or supply which change the equilibrium inflation rate will result in only a partial change in the observed inflation rate. We capture this inertia with an error-correction model:[6]
Δ is the difference operator, 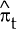 is given by equation (5) and
ut is an i.i.d. error which reflects shocks to the inflation rate. These might
include, inter alia, shocks to the price of oil and terms of trade and cyclical effects
on profit margins. The degree of inertia in the inflation process is determined by the
coefficients β and γ.
is given by equation (5) and
ut is an i.i.d. error which reflects shocks to the inflation rate. These might
include, inter alia, shocks to the price of oil and terms of trade and cyclical effects
on profit margins. The degree of inertia in the inflation process is determined by the
coefficients β and γ.
The error-correction model (13) admits a number of interesting special cases:
(i) β = γ = 1,
which implies 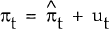 . This is the case of no inertia in the inflation
rate. Up to the error ut, inflation is always at its equilibrium rate.
. This is the case of no inertia in the inflation
rate. Up to the error ut, inflation is always at its equilibrium rate.
(ii) β = γ = 0,
which implies πt = πt−1 + ut. This is the case of complete inertia, with fundamentals having no effect on the inflation rate, which follows a random walk.
(iii) β = 0, γ = 1.
In this case,  i.e. the inflation rate is equal to the previous
period's equilibrium rate.
i.e. the inflation rate is equal to the previous
period's equilibrium rate.
(iv) β = 1, γ = 0,
which implies 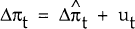 i.e. the change in the inflation rate is equal to the
change in the equilibrium rate, but the inflation rate itself need not be at its equilibrium
value.
i.e. the change in the inflation rate is equal to the
change in the equilibrium rate, but the inflation rate itself need not be at its equilibrium
value.
Footnotes
A recent instalment in this debate is the exchange between Hendry and Ericsson (1991) and Friedman and Schwartz (1991). [3]
A quantity theorist might contend that in the long-run institutions will adapt to make nominal wages endogenous and that the velocity of circulation will be determined by real factors, such as changes in transactions technology. Ultimately, money is then the only exogenous nominal variable and so its growth rate must determine the growth rate of the economy's numeraire i.e. money growth must cause price inflation. However, such a contention would be a tautology, not a theory of inflation. [4]
Specifically,  is weakly exogenous i.e. inference for the
model's parameters can be made conditionally on
is weakly exogenous i.e. inference for the
model's parameters can be made conditionally on  without
loss of information. For an extensive discussion of the various types of exogeneity
(weak, strong, strict and super), see Engle et al. (1983).
[5]
without
loss of information. For an extensive discussion of the various types of exogeneity
(weak, strong, strict and super), see Engle et al. (1983).
[5]
This specification can be derived as the optimum dynamic adjustment path for economic agents who minimize the discounted costs arising from the deviation of a variable from its equilibrium value. See Nickell (1985). [6]