RDP 9105: Inflation in Australia: Causes, Inertia and Policy Appendix 3: Tests for Serial Correlation and Heteroskedasticity

In Table 1, the abbreviations SC(1), SC(2) and SC(3) refer to the test statistics for first, second and third order serial correlation respectively.

Stewart (1986) outlines a Lagrange Multiplier test for serial correlation in a model which is linear in variables but non-linear in parameters.

Consider the model

where y_t is the dependent variable, g is the model specification with variables X_t and parameters b and u_t is the error term. The estimated model yields a series of parameter estimates and estimated errors . The individual error terms are standardised by subtracting their sample mean to produce the series .

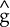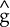The partial derivatives of g (denoted ) with respect to each of the parameters b are calculated and evaluated at the parameter estimates . The auxiliary regression (a2.2) of on and (the residual series lagged j times) is estimated to test for the presence of serial correlation specifically of the order j.

The test statistic is equal to T.R² where R² and T (the number of observations) refer to the estimation of equation (a3.2). This test statistic is distributed as χ²₍₁₎.

The abbreviations HS(1) and HS(2) in table 1 denote tests for different forms of heteroskedasticity of the residuals.

Stewart outlines how the Breusch-Pagan test can be used to test for heteroskedasticity related to a time trend (HS(1)) or the value of predicted dependent variable (HS(2)).

Using the error term series outlined above, equation (a3.3) is estimated:

where 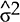is the sample variance of , Z_t is the variable potentially related to the heteroskedasticity of , κ₀ and κ₁ are parameters and u_t is an error term. For HS(1), Z_t is a time trend. For HS(2), Z_t is the predicted value of dependent variable in the primary estimation (from equation a3.1).

In both cases, the test statistic is equal to T.R² where R² and T (the number of observations) refer to the estimation of equation (a3.3). This test statistic is distributed as χ²₍₁₎.