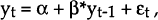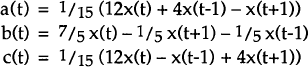RDP 9108: Australia's Real Exchange Rate – Is it Explained by the Terms of Trade or by Real Interest Differentials? Appendix

David W. R. Gruen and Jenny Wilkinson

September 1991

1. Unit Root Tests

The following tables contain the results of the unit root tests, divided up according to time period and frequency. The data from each series is assumed to be drawn from a model of the form

where εt has an ARMA(l,m) distribution. If β < 1, the series is stationary, while if β = 1, it is non-stationary (integrated of order 1). Three tests on each series are reported.

ADF is the augmented Dickey-Fuller test, as described in Said and Dickey (1984). Four lags on the differenced series (4 AR corrections) are included to absorb serial correlation. The null hypothesis for this test is non-stationarity.

Z(t) is the test proposed in Phillips (1987). This test involves making non-parametric adjustments to the ADF test. The null hypothesis for this test is also non-stationarity.

Since both the ADF and the Z(t) tests are widely recognised as having low power, we follow the recommendation of Pagan and Wickens (1989) and quote the coefficient estimate 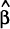Inline Equation as well as its test statistic, to give an indication of the estimated structural relationship.

G(p,q) is the test proposed by Park and Choi (1988). Unlike the other two tests, the null hypothesis for this test is stationarity. For all the tests in this paper, p = 0, and q = 5. Asymptotically, the G(p,q) statistic has a χ2(q-p) distribution.

For both the Z(t) and the G(p,q) test, we follow Phillips (1987) in using a Bartlett Window when estimating the long run variance. 10 lags on this window are used for both the quarterly and monthly data over the full sample periods, while only 5 lags were used for the quarterly over the shorter sample period.

***, **, * indicates the null is rejected at a 1%, 5%, 10% level of significance. (The relevant critical values are −3.43, −2.86, and −2.57 (Fuller, 1976) for the ADF and Z(t) tests and 15.09, 11.07 and 9.24 for the G(p,q) tests.)

QUARTERLY 1969:4 – 1990:4
SERIES RER TOT LONG
  Coeff Est Test Stat Coeff Est Test Stat Coeff Est Test Stat
Level
ADF 0.93 −1.54 0.87 −3.23** 0.83 −1.98
Z(t) 0.94 −1.87 0.93 −2.14 0.79 −3.02**
G(p,q)   6.30   5.53   7.65
First Difference
ADF 0.26 −3.12** 0.38 −3.70*** −0.52 −5.18***
Z(t) 0.02 −8.88*** 0.24 −7.26*** −0.08 −11.12***
G(p,q)   0.81   2.53   3.85
SERIES SHORT (B3) SHORT (F3) SHORT (B12)
  Coeff Est Test Stat Coeff Est Test Stat Coeff Est Test Stat
Level
ADF 0.48 −2.47 0.48 −2.76* 0.70 −2.72*
Z(t) 0.17 −7.98*** 0.21 −7.87*** 0.69 −3.91***
G(p,q)   7.21   7.47   6.88
First Difference
ADF −2.25 −5.81*** −2.15 −5.88*** −0.68 −4.90***
Z(t) −0.28 −22.95*** −0.38 −26.09*** −0.04 −11.95***
G(p,q)   7.69   4.42   4.79
QUARTERLY 1984:1 – 1990:4
  RER TOT TOT(C) LONG
  Coeff Est Test Stat Coeff Est rest Stat Coeff Est Test Stat Coeff Est Test Stat
Level
ADF 0.76 −1.71 0.81 −2.48 0.75 −2.48 0.78 −1.11
Z(t) 0.82 −2.10 0.93 −1.60 0.90 −1.66 0.75 −1.93
G(p,q)   6.40   5.74   5.86   6.07
First Difference
ADF 0.40 −1.69 0.64 −1.51 0.46 −1.52 −0.36 −2.29
Z(t) 0.02 −5.02*** 0.49 −3.03** 0.30 −3.81*** −0.06 −5.65***
G(p,q)   5.17   5.74   6.62   4.22
  SHORT (B3) SHORT (F3) SHORT (B12)
  Coeff Est Test Stat Coeff Est Test Stat Coeff Est Test Stat
Level
ADF 0.31 −1.41 0.35 −1.57 0.57 −1.97
Z(t) 0.10 −4.55*** 0.32 −3.66*** 0.66 −2.59*
G(p,q)   7.14   7.75   6.05
First Difference
ADF −2.25 −2.80* −2.08 −2.89** −0.53 −2.89**
Z(t) −0.39 −8.84*** −0.24 −8.01*** −0.17 −6.21***
G(p,q)   12.14**   5.12   5.96
MONTHLY 1984:12 – 1990:9
SERIES RERM TOTM (I) TOTM (C) TOTM (X)
  Coeff Est Test Stat Coeff Est Test Stat Coeff Est Test Stat Coeff Est Test Stat
ADF 0.95 −0.95 0.98 −1.30 0.95 −1.22 0.98 −0.70
Z(t) 0.89 −2.53 1.00 −1.03 0.96 −1.40 0.99 −0.74
G(p,q)   7.49   6.97   6.96   6.98
First Difference
ADF −0.25 −4.34*** 0.74 −2.11 0.15 −3.13** 0.44 −2.56
Z(t) −0.02 −8.47*** 0.61 −4.29*** −0.02 −8.51*** 0.09 −7.85***
G(p,q)   6.95   6.85   8.57   6.96
SERIES LONGM SHORTM (B3) SHORTM (F3) SHORTM (B12)
  Coeff Est Test Stat Coeff Est Test Stat Coeff Est Test Stat Coeff Est Test Stat
Level
ADF 0.91 −1.81 0.66 −3.17** 0.66 −3.03** 0.87 −1.83
Z(t) 0.94 −1.67 0.74 −2.88** 0.74 −2.88** 0.86 −2.43
G(p,q)   7.45   5.60   7.02   6.77
First Difference
ADF 0.06 −3.87*** −0.41 −4.83*** −0.32 −3.99*** −0.27 −3.71***
Z(t) 0.25 −6.31*** 0.21 −7.26*** 0.11 −8.28*** −0.01 −8.57***
G(p,q)   5.52   1.23   5.72   4.47

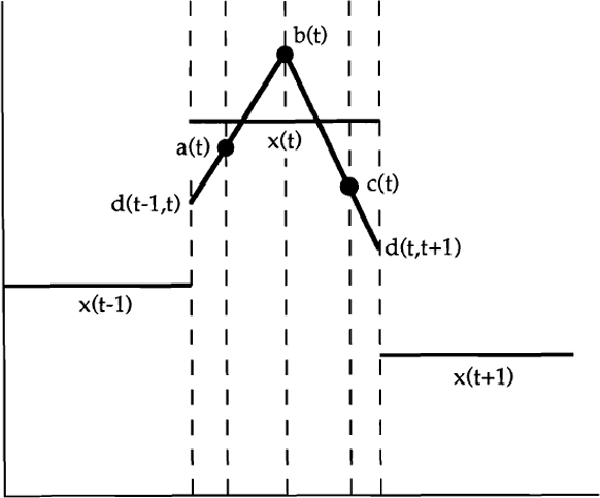
2. Interpolation of Quarterly-Period-Average Data

Define x(t) as the estimate for the series in quarter t; a(t), b(t), and c(t) as the consecutive monthly interpolated estimates in quarter t.

Define d(t,t+l) as the average of the current and next quarterly estimates,

Assumptions:

  1. The arithmetic average of the interpolated three months is the quarterly estimate,

  2. At the end of each quarter, the line joining the monthly interpolated estimates passes through d(t,t+1); and
  3. Each line segment d(t−1,t) b(t) and b(t) d(t,t+1) is a straight line segment.

Noting that the line segments d(t−1,t) a(t) and a(t) b(t) are in a ratio of 1:2, as are the line segments c(t) d(t,t+1) and b(t) c(t), equations (A1) and (A2) imply that:

This is represented diagrammatically by Figure 1.

Figure 1: Interpolation of Quarterly-Period-Average-Data
Figure 1: Interpolation of Quarterly-Period-Average-Data