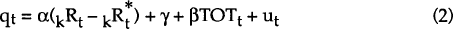RDP 9108: Australia's Real Exchange Rate – Is it Explained by the Terms of Trade or by Real Interest Differentials? 5. Discussion and Conclusions
September 1991
- Download the Paper 531KB
Four broad conclusions can be drawn from our results. First, they confirm the results of other studies (e.g. Blundell-Wignall and Gregory (1990), Corbae and Ouliaris (1991)) and accept the hypothesis that the Australian real exchange rate is non-stationary, rather than deviating only temporarily from purchasing power parity. However, we should again emphasise the low power of our statistical tests. For all the sample periods examined, both the null hypothesis of non-stationarity (using the ADF and Z(t) tests) and the null of stationarity (using the G(p,q) test) are accepted by the data.
Second, graphical analysis over the period 1969 – 1990 supports the evidence of Blundell-Wignall and Gregory (1990) in suggesting that there is a stable long run relationship between the Australian real exchange rate and the terms of trade (Graph 4). Perhaps surprisingly, the econometric tests provide only weak evidence supporting the existence of this stable long run relationship (Table 2). A possible explanation for this result is that other non-stationary variables are missing from the relationship. Plausible candidates are relative productivity growth and net foreign asset accumulation – both of which should have a longer-term impact on the real exchange rate. We briefly discuss these influences at the end of this section.
Third, over the period 1969 – 1990, the evidence does not suggest that short or long-term real interest differentials contribute to any stable long run relationship with the real exchange rate (Table 2).
Fourth, after the float of the $A and the world-wide deregulation of financial markets, there is evidence that real interest differentials do contribute to the behaviour of the real exchange rate. Although there is some evidence that short-term real differentials contribute to a stable relationship with the real exchange rate, the evidence is much stronger that long-term real interest differentials make a contribution.
After the float, three pieces of evidence which suggest that long-term real interest differentials contribute to a stable relationship with the real exchange rate are:
- There is stronger evidence for a cointegrating relationship between the real exchange rate and the long real interest differential on its own than between the real exchange rate and either short real differentials or the terms of trade on their own.
- There is good evidence of one (and sometimes more than one) stable relationship between the real exchange rate, the terms of trade and the long real interest differential. For most specifications, the t-statistics associated with the Phillips-Hansen estimates imply that the coefficient on the real long interest differential is statistically significant.
- For the six months after the end of the monthly estimation period, the long run relationship estimated using both TOTM(X) and LONGM seems to better explain the real exchange rate than either of these variables on their own or than SHORTM(B12) – see Graphs 5–7.
After the float, the evidence suggests that both the terms of trade and long real interest differentials contribute to a stable relationship with the real exchange rate. To estimate the magnitude of their influence on the real exchange rate, we use our preferred estimated relationship – with TOTM(X) and LONGM (Table 4 and Graph 6), and examine both Phillips-Hansen and Johansen estimates. Best estimates are that a 1% improvement in the terms of trade leads to an appreciation of the Australian real exchange rate of about 0.3 to 0.5%, while an increase of 1 percentage point in the differential between Australian and world long real interest rates is associated with an appreciation of the Australian real exchange rate of about 2 to 3½%.
Table 6 shows the size of changes in both the real exchange rate and simulations of our preferred long run relationship over the estimation period for the monthly data. As the Table illustrates, with this specification, long real interest differentials contributed more than the terms of trade to changes in the real exchange rate over both its depreciation and subsequent appreciation. However, an examination of Tables 3 and 4 demonstrates that different specifications yield significantly different coefficient estimates and hence relative contributions to exchange rate changes.
| Dec 84 – Dec 86 | Dec 86 – Sep 90 | |
|---|---|---|
| a. Our preferred estimated relationship – with TOTM(X) and LONGM
as explanators – is used in this simulation. b. The percentage points of change contributed by an explanator is calculated by simulating the long run model while holding the other explanator fixed at its initial level. As the model is non-linear in levels, the sum of individual contributions is not equal to the total estimated long run change. |
||
| Actual Real Exchange Rate (% change) | −25.9 | 22.7 |
| Long run estimate (% change) | −17.1 | 28.5 |
| Percentage points of change contributed by:b | ||
| Terms of trade (TOTM(X)) | −5.8 | 11.3 |
| Long real interest differential (LONGM) | −12.0 | 15.5 |
It is widely recognised that distinguishing between borderline stationary and non-stationary variables is a difficult exercise which is best attempted with long runs of data (see, for example, Frankel and Meese (1987)). From a theoretical perspective, in a world with deregulated financial flows, it is hard to understand how either short or long real interest differentials could be non-stationary. This would imply that real interest differentials should not appear in the long run relationship with the real exchange rate. The “true” long run (cointegrating) relationship would then be:
where a and b are positive constants and vt is a stationary error.
If equation (2a) represents the true long run model (with real interest differentials
stationary), OLS estimation of equation (2a) will generate a “super-consistent”
estimate of b. Under the same assumptions, the OLS estimate 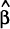 derived
from estimation of equation (2)
derived
from estimation of equation (2)
is also a super-consistent estimate of b.[19]
However, in small samples, there is no guarantee that equations (2) and (2a) will generate
similar estimates of b. This point is highlighted by a comparison of the coefficient estimates
on the terms of trade from estimates of the two equations. For example, from Table 4, estimation
of equation (2a) using TOTM(X) gives 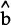 =
0.78 (E-G) or 0.82 (P-H), while estimation of equation (2) using TOTM(X) and LONGM gives
=
0.78 (E-G) or 0.82 (P-H), while estimation of equation (2) using TOTM(X) and LONGM gives 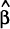 = 0.62
(E-G) or 0.51 (P-H) or 0.34 (Johansen). Thus, over the sample period, including the long real
interest differential in the regression substantially reduces the estimated influence of the
terms of trade on the real exchange rate.
= 0.62
(E-G) or 0.51 (P-H) or 0.34 (Johansen). Thus, over the sample period, including the long real
interest differential in the regression substantially reduces the estimated influence of the
terms of trade on the real exchange rate.
As discussed in Section 3(a) of this paper, economic theory implies that equation (2) is the correct specification. Given the short run of data, this leads us to have more confidence in the estimates derived from this equation than from equation (2a).
One can accept both the theoretical argument that long real interest differentials are stationary, as well as the empirical evidence that shocks to the long real interest differential persist for long enough to make the series appear non-stationary. The economic relevance of this argument is that while the real interest differential should not have a permanent effect on the level of the real exchange rate, its effect can last for an extended period – long enough to influence resource allocation between the traded and non-traded sectors of the economy.[20]
Note that the empirical observation that long real interest differentials appear non-stationary is not peculiar to Australia nor to our analysis being in trade-weighted terms. Bilateral studies of large OECD countries in Meese and Rogoff (1988) and Blundell-Wignall and Browne (1991) also come to this conclusion. There are two reasons why long real interest differentials may exhibit such strong persistence. The first relies on the Dornbusch (1976) argument that goods prices are sticky. Secondly, if monetary policy changes are not fully credible and/or if expectations are partly backward-looking, long real interest rates (as we measure them) may take considerable time to adjust to a change in the underlying inflation rate.
There is quite a strong correlation between short and long real interest differentials (with a correlation coefficient of 0.66 over the post-float period – see Table 1). So, high short real differentials are mostly associated with high long real differentials. Despite this fact, the relationships estimated in this paper are much more convincing with long rather than with short real interest differentials.
A possible explanation for the unsatisfactory results using short real differentials is that short-term nominal (and hence in a world with sticky inflation, real) interest rates are set by the authorities to achieve domestic economic objectives which change over time. Macfarlane and Tease (1989) point out that as well as having a medium-term inflation objective, short-term interest rates are used as a counter-cyclical stabilization tool and at times they have been used explicitly to support the exchange rate. These different roles for short interest rates presumably make it very difficult to uncover a stable relationship between short real interest differentials and the real exchange rate.[21]
The results in this paper are also consistent with those of Meese and Rogoff (1988) who find that their regressions (in first-difference form) are better with long real differentials rather than with short ones. Finally on this point, note that if inflationary expectations are rational, SHORT(F3) is an unbiased estimate of the expected short-term real interest differential. Since both our evidence and that of Meese and Rogoff is that SHORT(F3) is a stationary variable, it cannot (at least not on its own) form a stable long run relationship with the non-stationary real exchange rate.
To conclude, we briefly mention two further important determinants of the real exchange rate. First, over the longer run, inter-country differences in productivity growth make a profound difference to bilateral real exchange rates (see, for example, Dornbusch (1988)). The evidence of Broadbent (1991) and Lowe (1991) implies that labour productivity growth in the Australian traded sector in the 1970s and 1980s was significantly slower than the average labour productivity growth in the traded sectors of our major trading partners. Other things equal, this lower productivity growth implies a secular decline in the Australian real exchange rate.
Second, theory implies that other things equal, an increase (decrease) in a country's net holdings of foreign assets leads to an appreciation (a depreciation) of the domestic real exchange rate (see Dornbusch and Fischer, 1980, Meese and Rogoff, 1988). Hence, the increase in the ratio of Australia's net external liabilities to GDP from about 20% to about 40% over the 1980s should have put some downward pressure on the real exchange rate.
Empirically however, the link from a country's net foreign asset position to its real exchange rate appears to be a weak one. In the regressions run by Meese and Rogoff (1988), the estimated coefficient on the cumulated trade balance is of the wrong sign in four cases out of six (and always statistically insignificant). By contrast, the results of Blundell-Wignall and Browne (1991) are more encouraging – with the estimated coefficient on the cumulated current account of the correct sign in all cases. Interestingly for our purposes, during the financially deregulated 1980s, the cumulated current account had less than half the effect on the real exchange rate as in the more financially regulated 1970s. From their estimates, the increase – by 20% of GDP – in the Australian cumulated current account deficit during the 1980s should have been associated with a real depreciation of 4.4%.[22] The results in Table 6 imply that other influences – that is, terms of trade and real interest rate changes – had a substantially larger effect on the real exchange rate during the 1980s than this. Hence, it may prove difficult to isolate the effect of the cumulated current account deficit on the real exchange rate for Australia over the medium term.
Footnotes
As long as 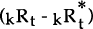 is uncorrected with ut, OLS
estimation of (2) also yields a consistent estimate of α.
[19]
is uncorrected with ut, OLS
estimation of (2) also yields a consistent estimate of α.
[19]
Meese and Rogoff (1988) point out that even if the series are borderline stationary, cointegration tests can still be meaningful, since they essentially test whether the large variance components of the different series effectively cancel each other, leaving a residual with only a small variance. [20]
Simes (1988) points out that this policy reaction function leads to a bias to the OLS coefficient estimate on the real interest differential. [21]
Derived as an average of results for Japan/US, Germany/US and Germany/UK from Table 4 of Blundell-Wignall and Browne (1991). [22]