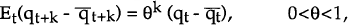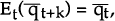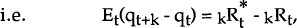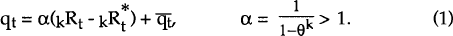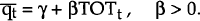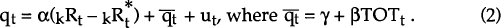RDP 9108: Australia's Real Exchange Rate – Is it Explained by the Terms of Trade or by Real Interest Differentials? 3. Methodology
September 1991
- Download the Paper 531KB
(a) Theoretical Motivation
In this paper we follow and extend the methodology of Meese and Rogoff (1988). As in their paper, we use real versions of the models proposed by Dornbusch (1976), Frankel (1979) and Hooper and Morton (1982).
There are three main assumptions behind these models. The first is that
where 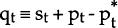 .
.
st is the nominal exchange rate (foreign currency price of domestic currency), pt
and 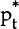 are
the domestic and foreign price levels, and qt is the real exchange rate, all measured
in logs. Et is the time-t expectations operator, θ is the speed of adjustment
parameter, and
are
the domestic and foreign price levels, and qt is the real exchange rate, all measured
in logs. Et is the time-t expectations operator, θ is the speed of adjustment
parameter, and 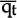 is the long run real exchange rate – that is,
the real exchange rate which would prevail at time t if all prices were fully flexible.
is the long run real exchange rate – that is,
the real exchange rate which would prevail at time t if all prices were fully flexible.
Thus after a temporary shock, the real exchange rate is assumed to move back to its long run equilibrium at a constant rate.
Secondly it is assumed that:
i.e. the long run real exchange rate is assumed to follow a martingale process or a random walk.
In Hooper and Morton (1982) 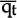 is posited to be a function of the
cumulated current account deficits of both countries (which are themselves assumed to be random
walks).
is posited to be a function of the
cumulated current account deficits of both countries (which are themselves assumed to be random
walks).
The third major assumption is that uncovered interest parity in its real form holds,
where kRt is the domestic real interest rate of maturity k at period t,
and 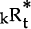 is the
corresponding foreign rate.
is the
corresponding foreign rate.
The combination of these three assumptions implies that the real exchange rate, qt, is determined in the following manner:
The assumptions imply that both qt and 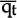 are
non-stationary variables, while
are
non-stationary variables, while 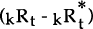 is a stationary variable. Changes
in the real interest differential are therefore expected to have only a temporary impact on the
real exchange rate. While securities of alternative maturity affect the magnitude of α,
they should not affect the underlying relationship between qt and
is a stationary variable. Changes
in the real interest differential are therefore expected to have only a temporary impact on the
real exchange rate. While securities of alternative maturity affect the magnitude of α,
they should not affect the underlying relationship between qt and 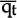 .
.
Equation (1) applies to the bilateral exchange rate between any two countries. As our focus is on the Australian trade-weighted real exchange rate, we study a trade-weighted version of equation (1). Rather than constructing a trade-weighted real interest differential, data limitations led us to use the differential between Australian real interest rates and an arithmetic average of real interest rates in the US, UK, Japan, and Germany.[3]
To extend this model we note that Blundell-Wignall and Gregory (1990) have shown that for a small open economy subject to terms of trade shocks, internal balance requires that the long run real exchange rate should be a function of the terms of trade. Hence in this paper, we posit that Australia's long run real exchange rate is a function of the terms of trade, that is,
Hence, our model for the real exchange rate is
We test four hypotheses:
- That the real exchange rate, qt, is non-stationary. The alternative hypothesis is that qt is stationary and hence that the real exchange rate exhibits only temporary deviations from purchasing power parity.
- That over the sample, there is a cointegrating relationship between the terms of trade and the real exchange rate.
- That over the sample, there is a cointegrating relationship between the real interest differential and the real exchange rate.[4]
- That over the sample, there is a cointegrating relationship between the real exchange rate and both the terms of trade and the real interest differential. In this case, we test if α > 1 and β > 0 as is required by the model underlying equation (2).
(b) Econometric Methodology
Over recent years, a number of techniques have been developed to establish whether stable long run (or cointegrating) relationships exist between non-stationary variables and to estimate these relationships. Probably the most widespread method used is the Engle-Granger (1987) procedure. This has the advantage of being straightforward to apply, relying as it does on single equation OLS estimation. However, it has two main limitations.
The first is that while coefficient estimates from the Engle-Granger procedure are “super consistent” (see, for example, Pagan and Wickens (1989) for a definition), inference cannot be made on these estimates because the t-statistics do not possess a t-distribution. This limitation can be overcome by making a non-parametric adjustment to the OLS coefficient estimates and standard errors (Phillips and Hansen (1990)). This procedure yields “fully modified” coefficient estimates with their associated t-statistics.
The second limitation of both the Engle-Granger (E-G) and Phillips-Hansen (P-H) procedures arises when there are more than two variables in a system. In this case, there may be more than one cointegrating relationship between them and the E-G and P-H approaches do not provide a method of examining this issue.
By contrast, the Johansen (1988) procedure[5] addresses the problem directly. It involves applying maximum likelihood techniques to estimate a full vector autoregressive system of equations which includes both levels and first differences. Note, however, that when more than one cointegrating relationship is identified, the estimated relationships are not unique, as any linear combination of the estimated relationships is also cointegrated.[6] In this case, interpretation is not so clear.
In this paper we make use of all these techniques. Before estimating the cointegrating relationships, we examine each series to see whether it is non-stationary in a unit-root sense. Three tests are used to assess a series' stationarity. The first (the Augmented Dickey Fuller [ADF] test, Said and Dickey (1984)) and second (the Z(t) test, Phillips (1987)) assume the null hypothesis that the series is non-stationary. The third test (the G(p,q) test, Park and Choi (1988)) assumes the null hypothesis that the series is stationary. All three tests suffer from low power – that is, it is common to accept the null hypothesis even when it is false.
Having established to our satisfaction that our series are non-stationary, we use the Engle-Granger and Phillips-Hansen procedures to estimate cointegrating relationships. In all cases, we allow for a constant in the cointegrating relationship, but no time trend. We apply two tests (the ADF and Phillips' Z(t) tests) to the residuals from the Engle-Granger regression to establish whether the series are cointegrated. Using the Phillips-Hansen estimation, we also apply Park's H(p,q) test for cointegration (Park (1988)).[7]
Finally, we apply the Johansen procedure. Where the real exchange rate is found to be cointegrated with both the terms of trade and real interest differentials, this gives us an indication of how many cointegrating relationships can be identified between the series.
(c) Series Used in Estimation[8]
| Quarterly Series: | |
| RER | log of Australia's real exchange rate with its 22 major trading partners, using quarterly average bilateral exchange rates and consumer price indices. |
| TOT | log of the terms of trade of goods and services. |
| TOT(C) | log of the ratio of the RBA Commodity Price Index (quarterly averages in $A) to the implicit price deflator for imports of goods and services. (Only available post-float.) |
| SHORT(F3) | expected short real interest differential using CPI inflation over the next quarter to proxy for expected inflation. |
| SHORT(B3) | expected short real interest differential using CPI inflation over the past quarter to proxy for expected inflation. |
| SHORT(B12) | expected short real interest differential using CPI inflation over the past year to proxy for expected inflation. |
| LONG | expected long real interest differential using CPI inflation over the past year to proxy for expected inflation. |
| Monthly Series[9]: | |
| RERM, SHORTM(B12) and LONGM are the monthly series equivalent to RER, SHORT(B12) and LONG respectively. Note however, that RERM is calculated using end month exchange rates. | |
| TOTM(I) | log of an interpolation of the quarterly terms of trade of goods and services. |
| TOTM(X) | log of the monthly Export Price Index deflated by an interpolation of the quarterly implicit price deflator for imports. |
| TOTM(C) | log of the RBA Commodity Price Index (in $A) deflated by an interpolation of the quarterly implicit price deflator for imports. |
Many alternative series could have been chosen for this exercise. In particular, the short and long real interest differentials can be calculated using different assumptions for inflationary expectations. A range of proxies for inflationary expectations have been proposed, from entirely backward-looking models to forward-looking models, to a mixture of the two. Campbell and Clarida (1987) compare survey data with a range of proxies for long-term inflationary expectations to illustrate how sensitive any calculation of the long-term real interest differential is to the proxy chosen. Mishkin (1987) agrees with their conclusions and states even more strongly that “research on the linkage between real interest rates and the exchange rate based on the examination of long-term real-interest differentials cannot be taken seriously.” (p. 143) Nevertheless, others continue to use such proxies. In this paper, we do not add to this debate, but we do follow others (Meese and Rogoff (1988)) in our use of such proxies.[10]
A number of different terms of trade measures are also used in this paper. The differences between these series is a combination of coverage, timing and periodicity.[11] While Simes (1988) argues that the real exchange rate should be determined by expected market prices, and hence expected commodity prices, rather than the prices exporters actually receive, this should only introduce a lag between the terms of trade and the real exchange rate due to the existence of contracts. Since the focus of this paper is on long run relationships, these short-term lags are presumably of less relevance.
Footnotes
An alternative would have been to trade-weight these four foreign real rates. The resulting series are almost identical to the series we use, and the estimation results are almost unchanged. [3]
This hypothesis requires that the real interest differential is non-stationary – which is contrary to the theory. We discuss this issue in the Discussion section. [4]
See Clements (1989) for a clear description of the Johansen procedure. For applied examples, see also Johansen and Juselius (1990). [5]
Assume that xt, yt and zt are three I(1) series with two independent cointegrating relationships between them: zt = α0 + α1 xt + α2 yt + ε1t and zt = β0 + β1 xt + β2 yt + ε2t with errors, ε1t and ε2t, which are I(0). A linear combination of these equations: zt = γα0 + (1 − γ) β0 + [γα1 + (1 − γ) β1] xt + [γα2 + (1 − γ)β2] yt + γε1t + (1 − γ) ε2t is also a cointegrating relationship since the error term in this new equation is a linear combination of the original I(0) errors and hence is also I(0). Thus γ can be chosen so that the coefficient on either xt or yt is zero. For a fully determined system, both cointegrating relationships must be specified. [6]
This test is similar to the G(p,q) test discussed earlier. We do not use the Durbin-Watson statistic to test for a cointegrating relationship because of its undesirable asymptotic properties (Phillips (1987)). [7]
The Data Appendix provides definitions and sources for the series. [8]
When it is necessary to derive a monthly series as an interpolation of a quarterly series, part 2 of the Appendix gives details of the interpolation. [9]
The strongest justification for our use of past 12 months inflation in calculating the long real interest differential is that inflationary expectations are adaptive. Some (see, for example, Blinder (1988) and Ball (1991)) regard this as the most reasonable assumption. Of course, this assumption may affect our estimation results, which we recognise as a lack of robustness of our analysis. [10]
The RBA Commodity Price Index includes 19 commodities and covers about sixty per cent of Australia's commodity exports, which is around forty per cent of Australia's total exports of goods and services. This series is very highly correlated with the implicit price deflator for exports of goods and services. Using quarterly data from September 1982 the correlation coefficient between the IPD for exports of goods and services and the Export Price Index is 0.998 and the correlation coefficient between the IPD for exports of goods and services and the RBA Commodity Price Index (all items in $A) is 0.976. [11]