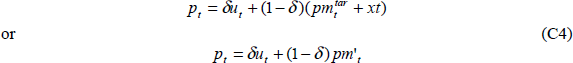RDP 2000-05: A Small Model of the Australian Macroeconomy Appendix C: Adjusting for Tariffs and the Balassa-Samuelson Effect

The import price faced by importers has been affected by the declining rate of tariff protection on imports into Australia over much of the sample period. We therefore define

where tariff_t is the average tariff rate on Australian imports (not its log), and the approximation ln(1 + tariff) ≈ tariff for small tariff rates has been invoked.

In the mark-up framework that forms the theoretical basis for the consumer price equation in the model, consumer prices are a mark-up over costs of production, that is, labour costs and the cost of imported goods. Assuming that the economy can be divided into traded and non-traded sectors, and that exportables are not consumed, the relevant costs are unit labour costs in the non-traded sector and import prices. In the long-run, therefore, we should have (up to a constant)

where u^NT is unit labour costs in the non-traded sector, and δ is the non-traded proportion of the economy. We make the common assumption, which underlies the Balassa-Samuelson effect, that the trend rate of labour productivity growth in the traded sector is higher than in the economy as a whole. As a consequence, unit labour costs rise more slowly in the traded sector than in the economy as a whole,

where u is economy-wide unit labour costs (as in the text) and x is the assumed difference between traded and economy-wide rates of productivity growth. Since 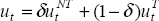, it follows from Equation (C3) that 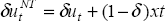, which may be substituted into Equation (C2) to give

where 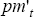are adjusted import prices, 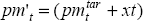, which we use in estimation of the consumer price equation in the text. Since the consumer price equation includes a constant, and since 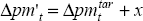, we also use the 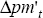series in place of the 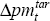series when the equation is estimated. As previously discussed, we restrict the sum of the coefficients on economy-wide unit labour costs and adjusted import prices to equal one (as required by Equation (C4)) when the consumer price equation is estimated.

We assume that the difference between the rate of labour productivity growth in the traded sector and the whole economy in Australia is the same as in the G7 economies. We therefore assume that x is given by the difference between consumer-price and export-price inflation in the G7, which is 2.1 per cent per annum over the period 1993:Q1–1999:Q3 (see Table 6).

As an alternative, it would be possible to estimate Equation (6) in the text by non-linear least squares assuming 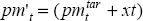, and thereby generating an estimate for x. When this is done, the resulting point estimate, 2.0 per cent per annum, is remarkably close to the value calculated from the data on the G7 economies. This point estimate is, however, statistically insignificant.