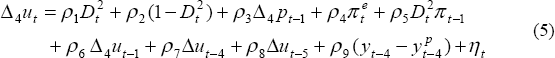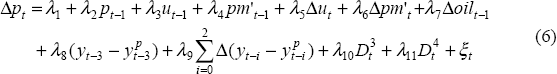RDP 2000-05: A Small Model of the Australian Macroeconomy 3. Equations
June 2000
- Download the Paper 535KB
In this section of the paper we present estimation results for the five equations in the model. The equations are estimated separately by ordinary least squares. The cross-equation variance-covariance matrix for the estimated residuals, reported in Appendix A, suggests that cross-equation correlations between these residuals are small in general and hence, that little is lost by estimating the equations individually rather than as a system. Furthermore, if one or other of the equations were mis-specified, single-equation estimation would avoid spreading this problem to the other equations in the system.
For each estimated equation, we follow a general-to-specific modelling approach. The equations are in equilibrium-correction form, with the exception of the unit labour cost equation, which is in first differences.[3] The sample period for all the equations is 1985:Q1–1999:Q3, which therefore excludes the more financially regulated 1970s and early 1980s.
We address the issue of the stability of the estimated equations in Appendix B. We test for a structural break at the beginning of 1993, after the low-inflation environment has been established. This is also around the time of an important change in monetary policy regime – the introduction of the medium-term inflation target. Appealing to the Lucas critique, this seems an appropriate time to test for possible structural breaks in the estimated equations. Our results do not show any obvious signs of instability around this time. It should be noted, however, that the sub-samples involved in this exercise are short and so many coefficients are imprecisely estimated, making it hard to draw definitive conclusions.
In all the estimations, variables are in logs, except for interest rates, and inflation expectations, which are expressed as per cent per annum, and the variable tariff, which appears in Appendix C. All variables in logs are multiplied by 100 so that their first differences are approximately in percentages. Appendix D provides a glossary of variables and a detailed description of the data and its sources.
3.1 Output
The single-equation representation of growth in Australian output is based on Gruen and Shuetrim (1994) and Gruen et al (1997). We use this specification of the output equation:
where y is Australian real non-farm GDP, yUS is real US GDP, s is a de-trended real share price accumulation index for Australian shares, ipOECD is real OECD industrial production and r is the real cash rate. We assume backward-looking inflation expectations so that the real cash rate is the nominal cash rate i less consumer price inflation over the past four quarters, rt = it −(pt − pt−4). The estimation results are shown in Table 1.
| Constant | −189.827*** (50.263) |
|---|---|
| Real cash rate (lags 2 to 7)(b) | −0.052*** {0.001} |
| Non-farm GDP (lag 1) | −0.389*** (0.090) |
| US GDP (lag 1) | 0.425*** (0.104) |
| De-trended real share prices (lag 1) | 0.045*** (0.010) |
| Non-farm GDP growth (lags 1 and 2)(c) | −0.201** (0.091) |
| OECD industrial production growth (lags 3 to 6)(c) | 0.089** (0.043) |
| Long-run elasticity – US GDP | 1.092*** (0.021) |
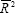
|
0.506 |
| Standard error of the residuals | 0.547 |
| F-test for joint significance of Australia and US GDP levels(d) | 14.491*** |
| LM tests for autocorrelation of residuals: | |
| First order | {0.073} |
| First to fourth order | {0.138} |
| Breusch-Pagan test for heteroskedasticity | {0.783} |
| Jarque-Bera test for normality of residuals | {0.456} |
|
Notes: (a) The equation is estimated by ordinary least squares using quarterly
data over the period 1985:Q1–1999:Q3. Numbers in parentheses () are
standard errors. Numbers in braces {} are p-values. ***, ** and * represent
significance at the 1, 5 and 10 per cent levels. All variables in log levels are
multiplied by 100 (so growth rates are in percentages). |
|
Following Gruen et al (1997), we include several lags of the real cash rate and do not eliminate insignificant intermediate lags. This allows flexibility in the estimated near-term pattern of the effect of monetary policy on output. The lagged coefficients on the real cash rate are negative, on average, and jointly highly significant.
Estimation of the equation confirms that foreign output has a powerful effect on Australian output growth. Table 1 shows that US GDP has a significant long-run effect on Australian output. Growth of industrial production in the OECD also helps to explain short-run dynamics in Australian output growth.
Following Fama (1990) and de Roos and Russell (1996), we include a de-trended measure of the cumulated return on Australian shares in the equation. Higher share prices raise shareholder wealth and lower the cost of equity, thereby leading to higher consumption and investment. The results suggest that share prices have a significant, and sizeable, impact on domestic output. A 10 per cent rise in the level of the accumulation index on Australian shares, sustained for a year, would raise output by 0.8 per cent over that time.
It would also be reasonable to expect that Australian output growth in the short run would rise with a rise in the terms of trade and fall with a rise in the real exchange rate. We find, however, that after controlling for the other explanatory variables in the equation, neither variable, in either levels or changes, has a significant effect on output growth. Given our uncertainty about the magnitude of the coefficients on these variables, and their limited role in explaining output growth in a freely estimated equation, these variables are excluded from the equation specification.
As a consequence of this exclusion, this equation cannot be used to estimate a monetary conditions index (as conventionally defined) for the Australian economy because there is no significant estimated effect on activity of changes in the real exchange rate.
Earlier versions of Equation (1) included growth in farm output as one of the explanatory variables. When current and lagged farm output growth are included in Equation (1), however, their contribution is small and insignificant.
We also experimented with alternative assumptions about inflation expectations. Rather than
assuming exclusively backward-looking expectations in the calculation of real interest rates (as
for the results in Table 1), we assumed that 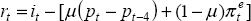 , where
µ is the assumed weight on backward-looking expectations, and
, where
µ is the assumed weight on backward-looking expectations, and 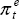 are inflation
expectations derived from the bond market. Estimating Equation (1) with this alternative
assumption for real interest rates, and varying the weight µ in the range 0 ≤
µ ≤ 1, made almost no difference to the goodness-of-fit of the equation (with
the adjusted R2 varying in a range of only 0.01).
are inflation
expectations derived from the bond market. Estimating Equation (1) with this alternative
assumption for real interest rates, and varying the weight µ in the range 0 ≤
µ ≤ 1, made almost no difference to the goodness-of-fit of the equation (with
the adjusted R2 varying in a range of only 0.01).
3.2 Real Exchange Rate
For a small, open economy such as Australia, the exchange rate is an important relative price. This explains the attention devoted to it in most Australian empirical macroeconomic models. Unfortunately, however, the exchange rate has proven persistently difficult to model both theoretically and empirically. For example, a common theory of exchange rate determination is uncovered interest rate parity, according to which an interest rate differential should reflect the expected future movement of the exchange rate. Empirical testing has, however, consistently rejected the joint hypothesis of uncovered interest parity and rational expectations, consistent with some form of foreign-exchange market inefficiency or time varying risk premia. Empirical modelling of the exchange rate has not been without its difficulties either. The classic Meese-Rogoff (1983) result – that for horizons up to a year, forecasts from economic models of the exchange rate are rarely any better than a ‘no-change’ forecast – suggests that the current exchange rate is about as good as any predictor of the future exchange rate, at least over short horizons.
Among existing models, there have been two approaches to modelling the Australian exchange rate. The first is based on an uncovered interest rate parity condition, assuming that market participants have rational expectations. Most large Australian macroeconometric models, including the Murphy and TRYM models (Powell and Murphy 1997; Douglas, Thompson and Downes 1997), follow this approach as does Svensson's (1998) simple stylised open economy model. The second common approach, and the one adopted here, is to model the exchange rate in a reduced-form, single-equation framework. This follows the work of Blundell-Wignall and Gregory (1990), Gruen and Wilkinson (1991), Blundell-Wignall, Fahrer and Heath (1993) and Tarditi (1996).
These papers have identified three fundamental determinants of the Australian real exchange rate: the terms of trade, the differential between domestic and foreign real interest rates, and net foreign liabilities. Over our sample, however, net foreign liabilities has an insignificant effect on the real exchange rate, so it is excluded from the specification of the equation.
The real exchange rate is modelled in an unrestricted equilibrium-correction framework which accommodates a long-run relationship between the real exchange rate and the terms of trade as well as short-run dynamics. We arrive at this parsimonious specification for the real exchange rate equation:
where θ is the Australian dollar against a trade-weighted average of the currencies of major trading partners, using consumer prices in each country to convert to a real exchange rate, tot is the terms of trade, r* is the foreign real interest rate (proxied by a weighted average of the real short-term policy rates in the G3 economies) and r has been defined earlier.[4] Over the estimation period, the Australian dollar was floating (the float began in December 1983). The estimation results are shown in Table 2.
| Constant | −2.019 (32.118) |
|---|---|
| Real exchange rate (lag 1) | −0.484*** (0.096) |
| Terms of trade (lag 1) | 0.473*** (0.124) |
| Real interest rate differential (lag 1) | 0.590** (0.252) |
| Terms of trade growth (lag 0) | 1.290*** (0.176) |
| Long-run elasticity – terms of trade | 0.977 (0.136) |
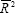
|
0.605 |
| Standard error of the residuals | 2.819 |
| F-test for joint significance of real exchange rate, terms of trade and real interest rate differential | 8.824*** |
| LM tests for autocorrelation of residuals: | |
| First order | {0.108} |
| First to fourth order | {0.449} |
| Breusch-Pagan test for heteroskedasticity | {0.048} |
| Jarque-Bera test for normality of residuals | {0.827) |
| Hausman (endogeneity) test(b) | −0.186 {0.611} |
|
Notes: (a) The equation is estimated by ordinary least squares using quarterly
data over the period 1985:Q1–1999:Q3. Numbers in parentheses () are
standard errors. Numbers in braces {} are p-values. ***, ** and * represent
significance at the 1, 5 and 10 per cent levels. All variables in log levels are
multiplied by 100 (so growth rates are in percentages). |
|
As one would expect, the interest rate differential is a significant determinant of the real exchange rate. Furthermore, a rise in the terms of trade appreciates the real exchange rate roughly one-for-one in the long run. The results suggest, however, that the exchange rate overshoots in the short-run.
A possible explanation for this overshooting is that the terms of trade are endogenous to the real exchange rate. Endogeneity may arise because changes in the exchange rate pass through to import prices faster than to export prices (Dwyer, Kent and Pease 1993), implying that exchange rate changes can cause terms of trade changes in the same direction that can persist for, perhaps, a year or so. Such endogeneity can bias the estimated relationship between contemporaneous changes in the real exchange rate and the terms of trade.
A response to this is to control for the possible simultaneity bias by using instrumental variables for the contemporaneous change in the terms of trade. Estimating such an instrumental variable regression, however, reveals little statistical evidence of simultaneity bias (see Table 2). Furthermore, there is minimal difference between the estimated coefficients in the instrumental-variable and ordinary-least-squares regressions (results not shown). In particular, instrumenting the terms of trade change does not reduce the extent of short-run overshooting of the real exchange rate.
3.3 Import Prices
Following Dwyer, Kent and Pease (1993) we model import prices in an equilibrium-correction framework, with the nominal exchange rate and foreign export prices as explanators. Our preferred specification is shown in Equation (3):
where pm is over-the-docks import prices in Australian dollars,
p*x is foreign export prices, and e is the nominal
exchange rate. The estimation results are shown in Table 3. The dummy, 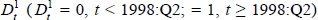 , and trend will
be discussed shortly.
, and trend will
be discussed shortly.
| Constant | 153.271*** (40.275) |
|---|---|
| Change in the nominal exchange rate (lag 0) | −0.657*** (0.030) |
| Change in the nominal exchange rate (lag 1) | −0.010** (0.046) |
| Change in foreign export prices (lag 0) | 0.567*** (0.212) |
| Change in foreign export prices (lag 1) | 0.389* (0.211) |
| Import prices (lag 1) | −0.335*** (0.089) |
| Foreign export prices (lag 1) | 0.335*** (0.089) |
| Nominal exchange rate (lag 1) | −0.335*** (0.089) |
| Trend | −0.108*** (0.026) |
| Dummy 1998:Q2–1999:Q3 | −2.796*** (0.699) |
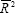
|
0.920 |
| Standard error of the residuals | 0.934 |
| F-test for joint significance of import prices, foreign export prices and nominal exchange rate | 17.959*** |
| LM tests for autocorrelation of residuals: | |
| First order | {0.092} |
| First to fourth order | {0.072} |
| Breusch-Pagan test for heteroskedasticity | {0.002} |
| Jarque-Bera test for normality of residuals | {0.030} |
| Test for static homogeneity (purchasing power parity) | {0.982} |
| Test for dynamic homogeneity | {0.0000} |
Notes: (a) The equation is estimated by ordinary least squares using
quarterly data over the period 1985:Q1–1999:Q3. Numbers in parentheses () are
standard errors. Numbers in braces {} are p-values. ***, ** and * represent
significance at the 1, 5 and 10 per cent levels. All variables in log levels are
multiplied by 100 (so growth rates are in percentages). |
|
Exchange rate data are available for all of Australia's trading partners, but relevant export price data are available for relatively few countries. We therefore estimate Equation (3) using GDP-weighted export prices from the G7 countries, and the nominal Australian dollar exchange rate against a GDP-weighted basket of G7 currencies.
We can view the G7 countries as setting a notional world price in global markets for goods and services. Of course, deviations from this price by non-G7 trading partners will not be captured by the equation. This has necessitated the addition of two extra variables in the equation: a time trend to capture the gradual shift in Australia's imports toward lower-priced goods from non-G7 countries (particularly in Asia), and a dummy variable since 1998:Q2 to capture extra price-undercutting by Asian exporters following the Asian crisis. The coefficients on both of these variables are negative and significant (see Table 3).
Two sets of restrictions on the equation are suggested by theory. The first is that traded goods prices should satisfy purchasing power parity in the long run (i.e., the equation should exhibit static homogeneity). This implies long-run elasticities of import prices with respect to foreign export prices and the nominal exchange rate of 1 and −1, or equivalently, ϕ2 = −ϕ3 = ϕ4. This restriction is easily accepted by the data, and imposed in the estimation.
The second set of restrictions is suggested by the idea that the margin between import prices
and the domestic-currency cost of imports, 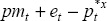 , should be unaffected by
changes in the steady-state rate of inflation. For the margin to be unaffected by a change in
the steady-state rate of domestic inflation which is matched by the same change in the
steady-state rate of depreciation (and the same change in the rate of import price inflation),
requires that
, should be unaffected by
changes in the steady-state rate of inflation. For the margin to be unaffected by a change in
the steady-state rate of domestic inflation which is matched by the same change in the
steady-state rate of depreciation (and the same change in the rate of import price inflation),
requires that 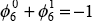 .
For the margin to be unaffected by a change in the steady-state rate of inflation of
foreign export prices, matched by an offsetting change in the steady-state rate of
depreciation, also requires that
.
For the margin to be unaffected by a change in the steady-state rate of inflation of
foreign export prices, matched by an offsetting change in the steady-state rate of
depreciation, also requires that 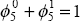 . These joint restrictions, which
together imply that the equation exhibits dynamic homogeneity, are overwhelmingly rejected by
the data and are not imposed (see Table 3).
. These joint restrictions, which
together imply that the equation exhibits dynamic homogeneity, are overwhelmingly rejected by
the data and are not imposed (see Table 3).
Adjustment of import prices to shocks in the explanatory variables is relatively fast, with two thirds of the adjustment to an exchange rate shock, for example, occurring within two quarters.
3.4 Unit Labour Costs
We use an expectations-augmented Phillips curve to model growth in unit labour costs. Inflation expectations are assumed to be a combination of backward- and forward-looking expectations. The backward-looking component combines lags of price and unit labour cost growth, while the forward-looking one is a measure of inflation expectations in the bond market, derived from the difference between the nominal and indexed 10-year bond yields. The output gap, rather than the unemployment gap, is used to capture wage-bargaining pressures.
Our parsimonious specification is shown in Equation (4).[5]
where u is unit labour costs, πe is the bond market's inflation expectations, and yp is potential output, calculated as described in Section 4.
We would expect on theoretical grounds that output could remain at potential at any steady rate of inflation, provided that steady rate was shared by consumer prices, unit labour costs and inflation expectations. That is, we expect Equation (4) to exhibit a vertical long-run Phillips curve (or, equivalently, to exhibit dynamic homogeneity).[6] This implies a restriction that the coefficients on the ‘inflation’ variables sum to one, that is ρ3 + ρ4 + ρ6 + (ρ7 + ρ8)/ 4 = 1. (The coefficients on quarterly changes are divided by four because the dependent variable is a four-quarter-ended change.)[7] The estimated coefficients sum to 0.74, and the restriction that they sum to one, as required, is overwhelmingly rejected by the data (see Table 4).
| Unrestricted(b) | Restricted(c) | |
|---|---|---|
| Constant | 0.539 (0.362) |
– |
| Dummy 1985:Q1–1995:Q4 | – | 0.304 (0.537) |
| Four-quarter-ended rate of inflation (lag 1) | 0.293*** (0.103) |
0.298*** (0.104) |
| Four-quarter-ended rate of unit labour cost growth (lag 1) | 0.481*** (0.110) |
0.473*** (0.110) |
| Quarterly unit labour cost growth (lag 4) | −0.961*** (0.131) |
−0.969*** (0.130) |
| Quarterly unit labour cost growth (lag 5) | −0.305** (0.115) |
−0.316*** (0.116) |
| Output gap (lag 4) | 0.537*** (0.114) |
0.528*** (0.114) |
| Bond market inflation expectations | 0.287*** (0.097) |
0.319*** (0.101) |
| Average inflation over past three years (lag 1) (1996:Q1 to sample end) | – | 0.231*** (0.084) |
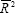
|
0.440 | 0.446 |
| Standard error of the residuals | 0.914 | 0.909 |
| LM tests for autocorrelation of residuals: | ||
| First order | {0.069} | {0.063} |
| First to fourth order | {0.178} | {0.182} |
| Breusch-Pagan test for heteroskedasticity | {0.834} | {0.677} |
| Jarque-Bera test for normality of residuals | {0.723} | {0.603} |
| Test for dynamic homogeneity | {0.0003} | |
| Test for dynamic homogeneity since 1996:Q1 | – | {0.573} |
| Test that quarterly model can be restricted to its four-quarter-ended form | – | {0.395} |
Notes: (a) The equations are estimated by ordinary least squares
using quarterly data over the period 1985:Q1–1999:Q3. Numbers in parentheses
() are standard errors. Numbers in braces {} are p-values. ***, ** and * represent
significance at the 1, 5 and 10 per cent levels. All variables in log levels are
multiplied by 100 (so growth rates are in percentages). |
||
The reason for this rejection is not immediately apparent. It may have something to do with the series of Accords between the Federal Government and the trade union movement in the 1980s and early 1990s, which are widely thought to have restrained growth in real unit labour costs at the time (Chapman 1990, Stevens 1992). The equation then ‘explains’ this period of restrained unit-labour-cost growth as a less than one-for-one response to the higher inflation at that time.
Whatever the reason for the rejection, we regard a vertical long-run Phillips curve as a sufficiently important property that we split the sample into two parts, and impose this constraint on the more recent sub-sample in a way that is accepted by the data. We estimate the specification shown in Equation (5).[8]
where 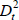 is a
dummy variable,
is a
dummy variable, 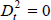 for t ≥ 1995:Q4,
for t ≥ 1995:Q4, 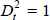 for
t ≥ 1996:Q1, and πt is the average rate of annual inflation
over the past three years, (pt −
pt−12)/3.
for
t ≥ 1996:Q1, and πt is the average rate of annual inflation
over the past three years, (pt −
pt−12)/3.
The joint restrictions that together imply a vertical long-run Phillips curve in the more recent
sub-sample are ρ1 = 0 and ρ3 +
ρ4 + ρ5 + ρ6 +
(ρ7 + ρ8)/4 = 1. The first of these restrictions
is imposed when the potential output series,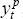 , is constructed (see Section 4) and the second, which
is easily accepted by the data, is imposed in estimation (see Table 4).
, is constructed (see Section 4) and the second, which
is easily accepted by the data, is imposed in estimation (see Table 4).
3.5 Consumer Prices
Following de Brouwer and Ericsson (1995), we model consumer prices as a mark-up over the unit input costs of production, which are assumed to be unit labour costs and import prices. Unit labour costs are the cost of domestic labour inputs, adjusted for labour productivity, while the inclusion of import prices reflects the cost of imported consumer, intermediate and capital goods. The mark-up is allowed to vary cyclically with the output gap, and is also influenced by oil prices. We adopt the following equilibrium-correction specification:
where pm′ is import prices adjusted for tariffs and for an assumed productivity
differential between the traded and non-traded sectors (as explained in Appendix C), and oil is the Australian dollar
price of crude oil. The dummy variables (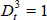 at 1990:Q4,
at 1990:Q4, 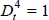 at 1991:Q1, 0
otherwise) allow for the huge, short-lived spike in oil prices at the time of the Gulf War,
which has an immediate, but temporary impact on consumer prices which the equation cannot
otherwise explain.
at 1991:Q1, 0
otherwise) allow for the huge, short-lived spike in oil prices at the time of the Gulf War,
which has an immediate, but temporary impact on consumer prices which the equation cannot
otherwise explain.
Estimation results are shown in Table 5. We test the equation for static homogeneity – the restriction that (up to a constant) consumer prices in the long-run are a linear combination of unit labour costs and adjusted import prices with the sum of the coefficients equal to one, that is λ2 = −(λ3 + λ4). This long-run restriction is accepted and imposed (see Table 5).[9]
| Constant | −0.541 (0.379) |
|---|---|
| Consumer prices (lag 1) | −0.073*** (0.008) |
| Unit labour costs (lag 1) | 0.043*** (0.013) |
| Adjusted import prices (lag 1) | 0.030*** (0.006) |
| Unit labour cost growth (lag 0) | 0.103*** (0.032) |
| Adjusted import price growth (lag 0) | 0.032** (0.013) |
| Oil price growth (lag 1) | 0.008*** (0.003) |
| Output gap (lag 3) | 0.142*** (0.026) |
| Change in the output gap (lags 0, 1 and 2 )(c) | 0.072** (0.032) |
| Dummy 1990:Q4 | 1.084*** (0.291) |
| Dummy 1991:Q1 | −1.254*** (0.290) |
| Long-run elasticity – unit labour costs | 0.585 (0.116) |
| – adjusted import prices | 0.415 |
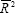
|
0.880 |
| Standard error of the residuals | 0.250 |
| F-test for joint significance of consumer price, unit labour cost and import price levels(d) | 74.100*** |
| LM tests for autocorrelation of residuals: | |
| First order | {0.832} |
| First to fourth order | {0.590} |
| Breusch-Pagan test for heteroskedasticity | {0.042} |
| Jarque-Bera test for normality of residuals | {0.366} |
| Test for static homogeneity | {0.087} |
| Test for dynamic homogeneity | {0.0001} |
Notes: (a) The equation is estimated by ordinary least squares using
quarterly data over the period 1985:Q1–1999:Q3. Numbers in parentheses () are
standard errors. Numbers in braces {} are p-values. ***, ** and * represent
significance at the 1, 5 and 10 per cent levels. All variables in log levels are
multiplied by 100 (so growth rates are in percentages). |
|
We also test for dynamic homogeneity – the restriction that the sum of the coefficients on ‘inflation’ terms is one, i.e., λ5 + λ6 + λ7 = 1. This restriction is overwhelmingly rejected by the data (see Table 5) and is not imposed. We discuss the relevance of this rejection in Section 5 of the paper.
The explanatory power of the equation is high, with an adjusted R2 of 0.88. Long-run elasticities of 0.58 and 0.42 on unit labour costs and adjusted import prices indicate that domestic input costs dominate total production costs. The output gap, as a measure of aggregate demand pressure, has a positive effect on prices as expected. The change in the gap, which measures the rate of change of output relative to potential, also helps to explain inflation in the near term.
Footnotes
The estimation techniques therefore generate consistent parameter estimates whether the variables in levels are non-stationary I(1) or borderline-stationary I(0) variables (provided the equation specifications are correct). The distributions of test statistics and some coefficient estimates would, however, differ somewhat in these two cases. [3]
We also experimented with commodity prices in place of the terms of trade in Equation (2). This was motivated by two observations. Most of the movement in the terms of trade is driven by commodity prices, given the large share of commodities in Australia's export basket. Furthermore, commodity markets are forward-looking, so it seems plausible that the exchange rate would respond to commodity prices rather than to the more sluggishly moving terms of trade. On the basis of goodness-of-fit, however, a model which includes the terms of trade was always superior to that with commodity prices. This result stood even when we used commodity prices only in the short-run dynamics. [4]
This model of four-quarter-ended changes in the dependant variable can be interpreted as a quarterly model with restrictions on the coefficients on the first three lags. We will return to this point shortly. The numbering of the coefficients contains gaps to ease later exposition. An equilibrium-correction term, ut−1 − pt−1, is insignificant when added to this equation or to Equation (5). [5]
Recall that we have assumed in estimation that the variables in levels are I(1) or borderline I(0), so that their growth rates are stationary I(0) variables. This assumption implies, for example, that the rate of unit labour cost growth cannot change permanently. However, we regard it as an important property of the model that unit labour costs and prices can grow at any constant rate in the steady state, and in principle that this steady-state rate of growth could change. Furthermore, that output in the steady state is independent of this rate of growth of costs and prices. To ensure these steady-state properties, it is necessary that the unit labour cost equation exhibit a vertical long-run Phillips curve. [6]
A vertical long-run Phillips curve would also require that the constant, ρ1, is zero. We return to this observation shortly. [7]
Estimating Equation (5) with quarterly rather than annual changes would imply the additional restrictions that the coefficients on Δut−1, Δut−2 and Δut−3 are all equal as are the coefficients on Δpt−1, Δpt−2, Δpt−3 and Δpt−4. These joint restrictions are easily accepted by the data (see Table 4). [8]
Since oil is also an input to production, we tested whether the oil price was part of the long-run relationship with consumer prices. When the lagged level of oil prices is added to the regression, its coefficient is of the correct sign but very small in magnitude and insignificant. We therefore excluded the oil price from the long-run relationship. [9]
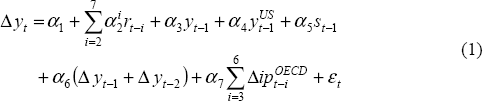
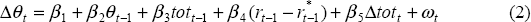
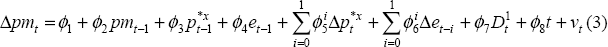
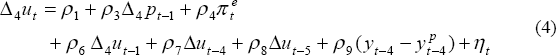
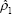 ,
is not reported, because the potential output series,
,
is not reported, because the potential output series, 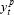 ,
is constructed so that
,
is constructed so that 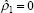 (see
(see