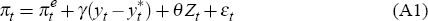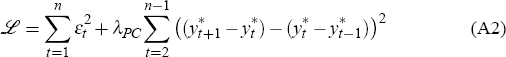RDP 2003-12: The Real-Time Forecasting Performance of Phillips Curves Appendix A: Construction of Real-time Output Gaps and Phillips Curves
December 2003
- Download the Paper 128KB
Gruen et al (2002) examine a range of univariate and multivariate methods for estimating the output gap in real time for Australia. They conclude that the best approach is to use an econometric technique based on inverting a Phillips curve, subject to a smoothness constraint. Since we use both the real-time output gaps and Phillips curves which they generate via this technique, we give a brief outline of it here. For a detailed description of the technique, see Gruen et al (2002).
Gruen et al start with an expectations-augmented Phillips curve of the form
where πt denotes quarterly core consumer price inflation (which has the
desirable property for real-time analysis that it is not revised); 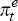 denotes inflation expectations; yt and
denotes inflation expectations; yt and 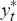 denote
actual and potential output (in logs); Zt represents a vector of other
variables (which may include changes in the output gap); and εt
denotes an error term.[35]
Then, for each vintage of data, they seek the smooth path for potential output that
gives the best fit to this Phillips curve. Formulated mathematically, this entails finding the
values for the parameter γ, the parameter vector θ, and the
potential output series {
denote
actual and potential output (in logs); Zt represents a vector of other
variables (which may include changes in the output gap); and εt
denotes an error term.[35]
Then, for each vintage of data, they seek the smooth path for potential output that
gives the best fit to this Phillips curve. Formulated mathematically, this entails finding the
values for the parameter γ, the parameter vector θ, and the
potential output series {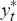 } which minimise the loss function
} which minimise the loss function
where, as in the usual H-P filter, λPC is a smoothing parameter to be chosen.[36]
For each data vintage, Gruen et al use a general-to-specific approach to choose an appropriate specification for the Phillips curve – as described in detail in Gruen et al (2002). Overall, the Phillips curve specifications selected vary only slowly over time. Table A1 lists these real-time specifications in full.
| Date of vintage | Precise equation specification |
|---|---|
| 1971:Q4 to 1972:Q4 | 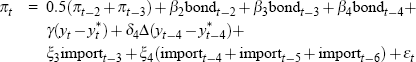 |
| 1973:Q1 to 1973:Q2 | 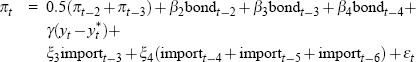 |
| 1973:Q3 |  |
| 1973:Q4 to 1974:Q2 | 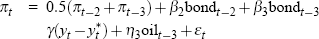 |
| 1974:Q3 | 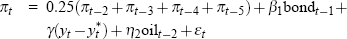 |
| 1974:Q4 to 1975:Q3 | 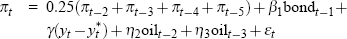 |
| 1975:Q4 to 1986:Q2 | 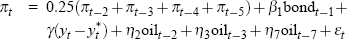 |
| 1986:Q3 to 1998:Q2 | 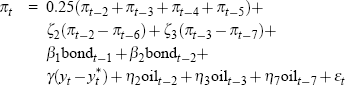 |
| 1998:Q3 to 2002:Q4 | 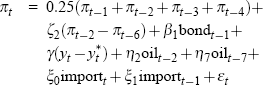 |
| Note: Start of sample for all regressions is 1961:Q2. | |
Footnotes
The Zt variables are constructed to be zero in the long run, so that the Phillips curve defined by Equation (A1) is vertical in the long run, with output at potential when inflation is equal to expected inflation. [35]
Details of the choice of λPC are set out in Gruen et al (2002). Note also that this loss function is similar to that underlying the conventional H-P filter, but with the sum of squared residuals from the Phillips curve in place of the sum of squared deviations of potential output from actual output. This has the desirable effect of building economic information into the filter: rather than potential output being penalised for differing from actual output in each period, such deviations are only penalised in Equation (A2) to the extent that they do not help to explain observed inflation. Incorporating economic information into the filter in this way also has the benefit that it reduces the end-point problems associated with H-P filters (since observed inflation then helps to determine the level of the output gap in each period more tightly). [36]