RDP 2003-12: The Real-Time Forecasting Performance of Phillips Curves 3. Methodology
December 2003
- Download the Paper 128KB
The starting point for our analysis is the paper by Gruen et al (2002), which provides a suite of 125 real-time Phillips curves and output-gap estimates, covering the data vintages from 1971:Q4 to 2002:Q4.[13] We wish to study the forecasting performance of these Phillips curves – focusing on the one-and four-quarter-ahead forecast horizons. However, we encounter an immediate methodological obstacle, namely: how should we handle the various explanators in our Phillips curves over the forecast period?
An important finding in Gruen et al (2002) was that, to generate reasonably reliable real-time output gaps using the filtering procedure adopted there, it is ‘important that the Phillips curve[s] be information-rich and as well specified as possible’ (p 32). Reflecting this, their preferred Phillips curves employ not just the output gap, but also a variety of other possible explanators of consumer price inflation. Often, these explanators enter their Phillips curves with a lag of less than four quarters, so that some assumption needs to be made about their future behaviour to enable out-of-sample inflation forecasts for the coming year to be generated in each period.[14] We now describe how we overcome this difficulty (by expanding our set of Phillips curves into a more general suite of two-equation forecasting models – consisting of a Phillips curve and an output-gap equation – one model for each data vintage). In Sections 3.2 and 3.3 we then describe a number of simple, alternative benchmark models for forecasting inflation.
3.1 A Suite of Phillips Curve-based Models for Forecasting Inflation
The Phillips curves from Gruen et al (2002) typically contain a contemporaneous output-gap term, as well as terms involving import price inflation, oil price inflation and bond market inflation expectations. We now specify how each of these explanators is to be extrapolated over the forecast period.
Forecasting the output gap
The explanator in our Phillips curves which is most likely to be the source of any real-time problems with forecasting inflation is the output gap. For this variable, our approach is therefore to assemble separate, estimated gap equations for each data vintage, using an approach similar to that used in Gruen et al (2002) to select our real-time Phillips curves. We now describe this approach in greater detail.
To obtain simple, estimated gap equations, we start with a general specification which includes, as explanatory variables: the real cash rate (rcash); changes in the terms of trade (Δtot); changes in the real trade-weighted exchange rate (Δrtwi); and a measure of the disequilibrium between the levels of the real exchange rate and the terms of trade (all with lags of up to 8 quarters).[15] Following Beechey et al (2000), we also include a de-trended real share accumulation index (rshare), to capture the share market's influence on real activity (for example, through wealth and confidence effects). The Southern Oscillation Index (soi) is also included as a possible explanator, as a proxy for the effects of the weather on the agricultural sector.
Prior to the mid 1980s, the Australian financial system was heavily regulated. As a result, the overnight cash rate is a less reliable indicator of the overall tightness or looseness of credit conditions for this period than for the post-deregulation era (Bullock, Morris and Stevens 1989). We therefore also experimented with adding to the general specification various alternative measures of the state of credit conditions. However, none of these variables were found to be consistently significant in any of our regressions.[16]
To arrive at our final specifications for each data vintage, both recursive regressions (in which the start date was held fixed at 1961:Q2) and 14-year rolling regressions were estimated. These regressions were used to sequentially eliminate variables on the basis of both t- and F-tests. Also, rather than conduct a new specification search for each new data vintage, we adopted the approach of revisiting our output-gap equation specifications: whenever significant deterioration was observed in the performance either of the overall equation or of its components; or, in any event, roughly every 10–12 years. Overall, this procedure was very similar to that used in Gruen et al (2002) to select our real-time Phillips curve specifications for each data vintage.
Ultimately, the specifications of our output-gap equations change only slowly over time. Table 1 shows the estimation results for our final vintage output-gap equation, estimated on 2002:Q4 data. All terms appear with the expected signs, and the regression standard error suggests that the equation does a fair job of explaining movements in the output gap over the past four decades.
| gapt = α + β1gapt − 1 + γ1rsharet − 1 + ϕ1soit − 1 + Ψ2(rcasht − 2 + rcasht − 3 + … + rcasht − 7) + εt | ||
|---|---|---|
| Coefficient | Value | t-statistic |
| α | 0.0016 | 1.1514 |
| β1 | 0.8705 | 27.1327 |
| γ1 | 0.0255 | 3.5064 |
| ϕ1 | 0.0002 | 2.1276 |
| Ψ2 | −0.0138 | −2.1278 |
| Summary statistics | Value | |
| R2 | 0.8947 | |
| Adjusted R2 | 0.8921 | |
| Standard error of the regression | 0.0117 | |
| Breusch-Godfrey LM test for autocorrelation (p-value): | ||
| First order | 0.2590 | |
| First to fourth order | 0.1845 | |
|
Note: The sample is 1961:Q2 to 2002:Q4 (n = 167). |
||
The real-time output-gap equation specifications for our complete set of 125 data vintages are summarised in Table 2, and are set out in full in Appendix B. Several characteristics of the specifications in Table 2 stand out. First of all, the first lag of the gap itself appears in every equation vintage (with the fifth lag also appearing in specifications for the late 1970s and most of the 1980s). Fairly consistent roles are also found for: the de-trended real share accumulation index lagged one period; one or more lags of the quarterly change in the real trade-weighted exchange rate (except in early and late equation vintages); and the first lag of the Southern Oscillation Index (except in early vintages). Finally, an explicit role for lags of the real cash rate is only identified for equation vintages in the post-financial deregulation era, specifically from December quarter 1985 onwards.[17]
| Date of vintage | Broad equation specification |
|---|---|
| 1971:Q4 to 1978:Q1 | 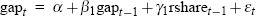 |
| 1978:Q2 to 1985:Q3 | 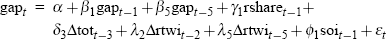 |
| 1985:Q4 to 1989:Q1 | 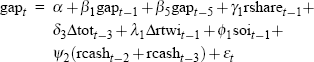 |
| 1989:Q2 to 1995:Q2 | 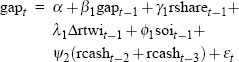 |
| 1995:Q3 to 2002:Q4 | 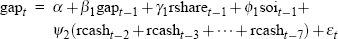 |
|
Note: Start of sample for all regressions is 1961:Q2. |
|
Extrapolating explanators other than the output gap
For all variables other than the output gap, our approach is simply to assume perfect foresight on the part of our forecasters, in each period. In other words, we assume that in each period our forecasters, although uncertain about the future trajectories of consumer price inflation and the output gap, know precisely how such variables as oil and import price inflation, bond market inflation expectations, and the Southern Oscillation Index, will develop over the coming year.
The obvious alternative to this approach would have been to construct real-time models in each quarter for the evolution of all these variables (as well as any other explanators which, in turn, arose in the equations for these variables). However, with 125 vintages of data, such an approach was beyond the scope of this project. Moreover, none of these variables is subject to serious real-time measurement problems, the implications of which are the focus of this paper.
Nevertheless, our assumption of perfect foresight, in relation to these variables, should be borne in mind in the discussion of our results in Section 4. It certainly imputes to our Phillips curve-based forecasters, in each period, unrealistic prescience about these inputs to their forecasts – and so presumably biases our results somewhat in favour of our Phillips curve-based forecasting approach.
Summary
In summary, we now have a small, estimated suite of models, one for each data vintage from 1971:Q4 to 2002:Q4, consisting of: a Phillips curve from Gruen et al (2002); an output-gap equation; and the assumption of perfect foresight on the part of forecasters with regard to oil and import price inflation, bond market inflation expectations, and the various explanators arising in that vintage's gap equation (such as the nominal cash rate, the Southern Oscillation Index, and so forth). For each period we use this model to generate real-time inflation forecasts at one- and four-quarter-ahead horizons. This constitutes our Phillips curve-based approach to forecasting Australian consumer price inflation.
3.2 Alternative Benchmark Models for Forecasting Inflation
To judge the real-time performance of our Phillips curve-based approach to forecasting inflation, we need some benchmarks against which we can compare its performance. We consider two alternative, univariate benchmarks: a ‘no-change’ assumption for inflation; and an autoregressive (AR) model of inflation.
The former treats inflation as a random walk.[18] The latter models inflation in terms of the first two lags of itself (together with a constant), with the equation re-estimated for each data vintage. In selecting this general specification we allowed, in principle, for longer lags of inflation. However, we found that the autocorrelation and partial autocorrelation functions for inflation regularly suggested focusing on the first three lags, and that the performance of an AR(2) model was typically closely comparable to that of an AR(3). Hence we preferred the slightly more parsimonious AR(2) specification.[19]
3.3 Two Further Benchmarks for Comparison
As a further reference point for assessing the performance of our suite of Phillips curve-based models, we also consider the forecasting performance of our final vintage (2002:Q4) Phillips curve, estimated on final data. By this we mean the results which would have been achieved by a forecaster who, in each quarter of the evaluation period, happened to know in advance: the final, 2002:Q4 vintage Phillips curve specification, including its ‘true’ coefficient values (as estimated on final data); the ‘true’ (final vintage) profile of the output gap up to that period; and, finally, the correct future paths of oil prices, import prices, bond market inflation expectations, and the output gap, over the year ahead. In Sections 4 and 5, we refer to these simply as the ‘final vintage Phillips curve’ forecasting results. Likewise, we also consider the corresponding forecasting performance of our ‘final vintage (2002:Q4) AR model’.
Footnotes
The way in which these Phillips curves were selected, and corresponding vintages of output-gap data generated, was described in detail in Gruen et al (2002). It is summarised briefly in Appendix A, which also contains a complete listing of these specifications. Note that Gruen et al actually provides only 121 Phillips curves. We have increased this number to 125 by also applying the final Phillips curve from Gruen et al to the four data vintages from 2002. In arriving at this specification for these additional vintages we applied the same specification search procedure as that used to obtain the original 121 Phillips curves in Gruen et al. [13]
This difficulty does not arise in Orphanides and van Norden (2003) because their forecasting Phillips curves do not include explanators other than the output gap and lags of inflation itself. Moreover, the output gap is not allowed to enter their Phillips curves with a lag less than the length of their inflation forecast horizon, so that they even avoid the need to extrapolate the output gap into the forecast period. While this simplifies the construction of their real-time inflation forecasts, it raises the question: do these constraints on the specifications of their Phillips curves bias their results against finding a role for these curves in forecasting inflation? [14]
Note that, for each period, to generate our short-term real interest rate data we use the inflation expectations measure implicit in the Phillips curve specification for that vintage. This is done to ensure consistency in the measure of inflation expectations used within our model. This measure computes inflation expectations as a linear combination of lagged inflation and bond market inflation expectations, with the weights for each vintage being the coefficients estimated in the Phillips curve – see Gruen et al (2002) for further details. This adds a real-time aspect to our measure of inflation expectations, since these weights evolve slowly over time. [15]
The variables we experimented with included: the quarterly change in the Statutory Reserve Deposit (SRD) ratio, the proportion of their deposits which trading banks were, until August 1988, required to hold at the Reserve Bank as cash reserves; the 90-day bank bill rate; and a ‘weighted interest rate’ (constructed as an average of the prevailing interest rates for different debt maturities, weighted by the proportion of total credit outstanding at these maturities). Real-time data issues ruled out consideration of a number of other, otherwise plausible candidates, such as various monetary aggregates. [16]
Our failure to find an explicit role for some measure of conditions in credit markets, in the pre-deregulation era, may reflect our inability, discussed earlier, to identify a good, single summary indicator for this variable for this period. [17]
Strictly speaking, we actually use two distinct random walk models, one for quarterly and one for year-ended inflation. In other words, in each period we assume: that quarterly inflation in the coming quarter will be the same as in the current quarter; and that year-ended inflation over the coming year will be the same as over the year to the current quarter. [18]
We also considered using a more general ARMA model, to allow for a possible indeterministic (moving average) component which might be useful in better capturing the persistence in inflation. However, while an ARMA(1,1) model also generally works well, it does not outperform our chosen AR(2) specification, which we therefore preferred as marginally simpler and more intuitive. [19]