RDP 2003-12: The Real-Time Forecasting Performance of Phillips Curves 5. Why Do Our Phillips Curves Forecast Poorly?
December 2003
- Download the Paper 128KB
In Section 4 we saw that the capacity of our real-time Phillips curve-based models to forecast inflation is disappointing, relative to some simple alternatives. We now try to identify what factors are responsible for this poor performance.
Recall that our Phillips curve-based forecasts have perfect foresight built into them with regard to variables such as oil and import prices, and bond market inflation expectations. This leaves two main candidates for the source of errors in these forecasts.
One is that our real-time estimates of the output gap are subject to error, which may be directly contributing to problems with our Phillips curve-based forecasts of inflation. Errors in historical estimates of the gap in any given quarter feed through to corresponding errors over the forecast period. These, in turn, affect our Phillips curve-based inflation forecasts – even in the absence of any specification or coefficient estimation problems in the Phillips curve or gap equation for that quarter. The other possibility is that, in part because of real-time problems with estimating the gap, our Phillips curves and gap equations themselves may be flawed, either through mis-specification or mis-estimation of parameters.[30]
To assess which of these two factors may be the more important, we introduce two alternative suites of ‘intermediate models’, both of which lie between our real-time Phillips curve-based models and our final vintage Phillips curve. For the first of these sets of intermediate models, in each period we use the same Phillips curves and output-gap equations, estimated on that period's data, as in our real-time Phillips curve-based models. However, we use the final vintage data for the gap (and for inflation expectations) up to that period, in generating forecasts for inflation over the year ahead. In terms of bridging the gap between our real-time Phillips curve-based models (real-time equations and real-time data) and our final vintage Phillips curve (final equations and final data), this first set of intermediate models may therefore be thought of as representing ‘real-time equations but final data’.
Our second set of intermediate models simply reverses the order in which the gap between our real-time Phillips curve-based models and final vintage Phillips curve is bridged, using instead ‘final equations but real-time data’. Specifically, for this second set of intermediate models we therefore use, in each period, the final vintage Phillips curve and output-gap equation, as estimated on final vintage data. However, we use real-time data for the gap (and for inflation expectations) up to that period, in generating forecasts for inflation over the year ahead. A comparison of the forecasting performance of these two sets of intermediate models with that of our real-time and final vintage Phillips curves is provided in Table 7.
| Method | Final vintage PC | Intermediate models (I) | Intermediate models (II) | Real-time PC |
|---|---|---|---|---|
| Real-time eqns, final data | Final eqns, real-time data | |||
| Forecasts for quarterly inflation (one quarter ahead) | ||||
| RMSE | 0.31 | 0.44 | 0.32 | 0.44 |
| Bias | 0.01 | −0.02 | 0.03 | −0.01 |
| Forecasts for year-ended inflation (one year ahead) | ||||
| RMSE | 0.87 | 1.59 | 1.03 | 1.55 |
| Bias | 0.08 | −0.05 | 0.22* | 0.03 |
|
Notes: Results are calculated over the forecast sample period 1976:Q1 to 2002:Q4. ‘RMSE’ is the root mean squared error between actual inflation and the series of real-time inflation forecasts generated by the method shown, in percentage points; ‘Bias’ is the average percentage point error in the forecast series over the evaluation period. * indicates that the bias is significant at the 5 per cent level. |
||||
Interestingly, we see that, on average over the whole sample from 1976:Q1 onwards, our first set of intermediate models performs no better (in RMSE terms) in forecasting inflation than our real-time Phillips curve-based models, at either the one- or four-quarter-ahead horizons. It appears that, if forced to work with Phillips curves estimated in real time, then one may as well continue to use the same flawed, real-time output-gap data used in the equation specification and estimation process, when forecasting inflation. Doing so produces forecasts which perform as well as predictions based on more accurate gap information, determined using revised output data and with the benefit of hindsight.
By contrast, while our second set of intermediate models performs worse in forecasting inflation than our final vintage Phillips curve, it does markedly better than our real-time Phillips curve-based models. This is true, in RMSE terms, at both the one- and four-quarter-ahead horizons – although, at the latter horizon, the forecasts from our second set of intermediate models do exhibit some bias.
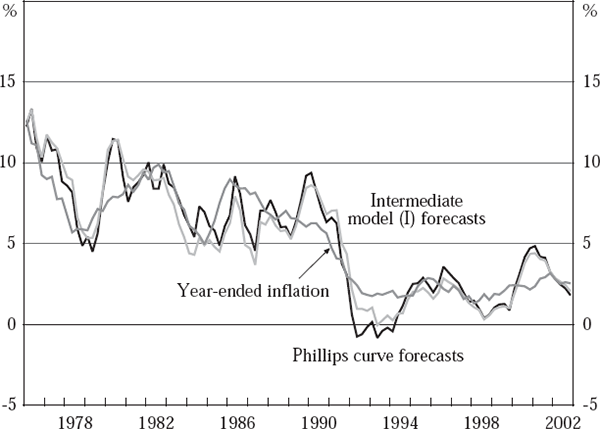
In combination, these results strongly suggest that the principal problem with the use of Phillips curve-based models to forecast inflation in real time lies in identifying the correct specification and coefficient estimates for the model equations. By contrast, the direct effects of output-gap mis-estimation on the inflation forecasts seem relatively unimportant – a finding which aligns with that of Orphanides and van Norden (2003) for the US.[31] There have, however, been particular periods where the direct effects of gap mis-estimation have been important, such as the early 1990s recession (already discussed in Section 4.2). The persistent mis-estimation of the output gap during this period, by around 3 percentage points, is a major source of errors in our real-time Phillips curve-based forecasts for year-ended inflation for this period – as illustrated by Figure 5, which compares these forecasts (real-time equations, real-time data) with those from our first set of intermediate models (real-time equations, final data).
Footnotes
It is also possible that a number of other factors may be contributing to the disappointing performance of our real-time Phillips curve-based forecasts. Such factors include our imposition of a long-run verticality condition on our Phillips curve specifications, and our choice of output-gap measure. However, for the US, Orphanides and van Norden (2003) find that the relative forecasting performance of output-gap-based Phillips curves with and without a long-run verticality condition imposed is about the same. Likewise, their results for the US suggest that our choice of output-gap measure is unlikely to be responsible for the unimpressive forecasting performance of our real-time Phillips curves: they examine a dozen alternative gap measures, and find all of them to be of generally low value in helping to predict inflation in real time. Moreover, it would be problematic, on other grounds, for us to switch to an alternative approach to estimating the gap, so as to try to improve our capacity to forecast inflation using Phillips curves, since the results of Gruen et al (2002) suggest that any gain on this front would be likely to come only at the cost of worse real-time reliability of the estimates of the gap itself. [30]
Orphanides and van Norden observe that their results ‘provide no evidence to suggest that the relative inaccuracy of [their various] real-time gaps is responsible for their poor forecasting performance’, but rather suggest ‘quantitatively important instability in the relationship between output gaps (however measured) and inflation’ (p 16). [31]