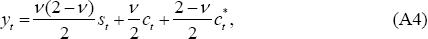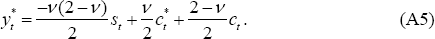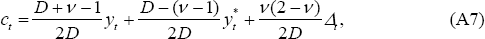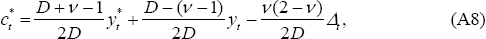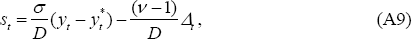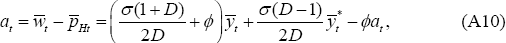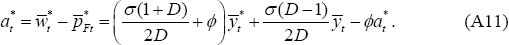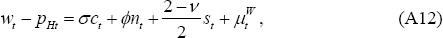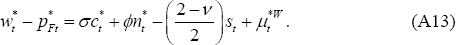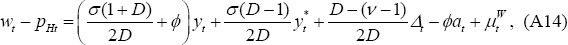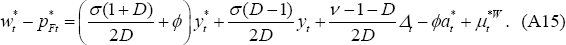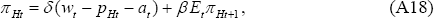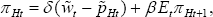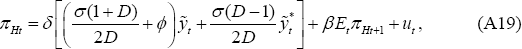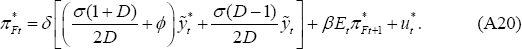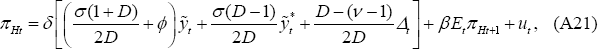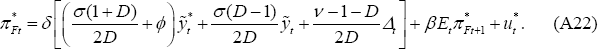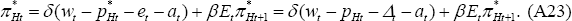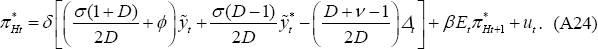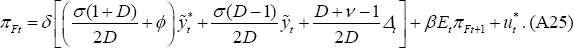RDP 2009-01: Currency Misalignments and Optimal Monetary Policy: A Re-examination Appendix A: Log-linearised Model
March 2009
- Download the Paper 512KB
The log-linear approximations to the models presented above are presented in this Appendix.
Use is made of the first-order approximation  ,
as explained in the text. That relationship is obvious in the flexible-price
and PCP models, but will require some explanation in the LCP case. That explanation
is postponed until later.
,
as explained in the text. That relationship is obvious in the flexible-price
and PCP models, but will require some explanation in the LCP case. That explanation
is postponed until later.
In this Appendix, all of the equations of the log-linearised model are presented, but those that are used in the derivation of the loss function (which do not involve price setting or wage setting) are separated from those that are not.
Equations used for derivation of loss functions
The log of the deviation from the law of one price is defined as:
In the flexible-price and PCP models, Δt = 0. In the LCP model, because  , the law of one price
deviation is the same for both goods:
, the law of one price
deviation is the same for both goods: 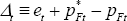 .
.
In all three models, to a first order, 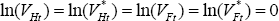 .
That allows Equation (23) and its foreign counterpart to be approximated as:
.
That allows Equation (23) and its foreign counterpart to be approximated as:
The market-clearing conditions, (18) and (19) are approximated as:
The condition arising from complete markets that equates the marginal utility of nominal wealth for home and foreign households, Equation (22), is given by:
For use later, it is helpful to use Equations (A4)–(A6) to express  ,
in terms of yt and
,
in terms of yt and  and the exogenous
disturbances,
and the exogenous
disturbances,
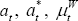 ,
and
,
and 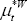 :
:
where D ≡ σv(2 − v) + (v − 1)2.
Under a globally efficient allocation, the marginal rate of substitution between
leisure and aggregate consumption should equal the marginal product of labour
times the price of output relative to consumption prices. To see the derivation
more cleanly, insert the shadow real wages in the efficient allocation, 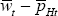 and
and 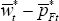 into Equations (A10) and (A11) below. So, the efficient allocation would be achieved
in a model with flexible wages and optimal subsidies. These equations then
can be understood intuitively by looking at the wage-setting equations below
(Equations (A14)–(A15), and (A16)–(A17)) assuming the optimal
subsidy is in place. But they do not depend on a particular model of wage
setting, and are just the standard efficiency condition equating the marginal
rate of substitution between leisure and aggregate consumption to the marginal
rate of transformation.
into Equations (A10) and (A11) below. So, the efficient allocation would be achieved
in a model with flexible wages and optimal subsidies. These equations then
can be understood intuitively by looking at the wage-setting equations below
(Equations (A14)–(A15), and (A16)–(A17)) assuming the optimal
subsidy is in place. But they do not depend on a particular model of wage
setting, and are just the standard efficiency condition equating the marginal
rate of substitution between leisure and aggregate consumption to the marginal
rate of transformation.
Equations of wage and price setting
The real home and foreign product wages, from Equation (38), are given by:
wt − pHt and 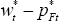 can be expressed in
terms of yt and
can be expressed in
terms of yt and 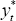 and the exogenous
disturbances,
and the exogenous
disturbances,
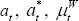 ,
and
,
and 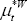 :
:
A.1 Flexible Prices
The values of all the real variables under flexible prices can be solved by using Equations (A2), (A3), (A7), (A8), (A9), (A14) and (A15), as well as the price-setting conditions, from (43):
A.2 PCP
Log-linearisation of Equations (49) and (50) leads to the familiar New Keynesian Phillips curve for an open economy:
where δ = (1 − θ)(1 − βθ)/θ.
This equation can be rewritten as:
or, using (A14) and (A10):
where 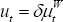 .
.
Similarly for foreign producer price inflation:
A.3 LCP
Equation (A18) holds in the LCP model as well. But in the LCP model, the law of one price deviation is not zero. It follows that:
In addition, Equations (18) and (51) imply:
This can be rewritten as
Similarly:
From Equations (A7)–(A8) and (A14)–(A15), it can be seen that  .
Assuming a symmetric initial condition leads to the conclusion that
.
Assuming a symmetric initial condition leads to the conclusion that  as noted above. That
is, the relative price of foreign to home goods is the same in both countries.
I emphasise that this is true in general for a first-order approximation.
as noted above. That
is, the relative price of foreign to home goods is the same in both countries.
I emphasise that this is true in general for a first-order approximation.