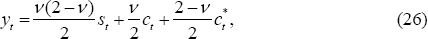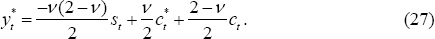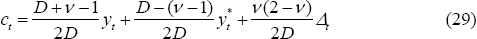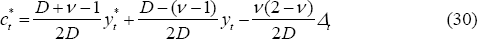RDP 2009-01: Currency Misalignments and Optimal Monetary Policy: A Re-examination 3. Log-linearised Model

This section presents some log-linear approximations to the models presented above. The full set of log-linearised equations appears in Appendix A. The approach to the optimal policy decision is to consider a second-order approximation of the welfare function around the efficient steady state. The derivation of the loss function itself requires a second-order approximation of the utility function itself, but in the course of the derivation will actually require second-order approximations to some of the equations of the model. However, for many purposes, the first-order approximations are useful: the constraints in the optimisation problem need only be approximated to the first order; the optimality conditions for monetary policy – the ‘target criteria’ – are linear; and, the dynamics under the optimal policy can be analysed in the linearised model.

With regard to notation, lower case letters refer to the log of the corresponding upper case letter less its deviation from steady state.

If firms set the same price for home and foreign consumers, then . To a first order, is assumed even if firms set different prices in the two countries. That is, for the aggregate price indices, 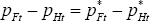, so relative prices are the same in the home and foreign countries. This relationship will turn out to hold in the Calvo pricing model under LCP, when the frequency of price adjustment is identical in the two countries.

The log of the deviation from the law of one price is defined as:

Because , the deviation of the law of one price is the same for both goods: .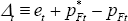

The market-clearing conditions, (18) and (19), are approximated as:

The condition arising from complete markets that equates the marginal utility of nominal wealth for home and foreign households, Equation (22), is given by:

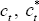, and s_t can be expressed in terms of 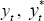and Δ_t:

where D ≡ σv(2 – v) + (v – 1)².

The model is closed and solutions for the endogenous variables can be derived once policy rules are determined. I now turn to consideration of optimal monetary policy.