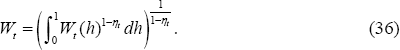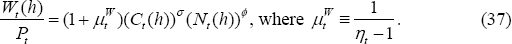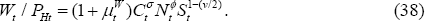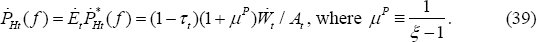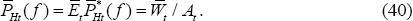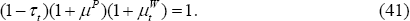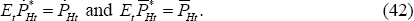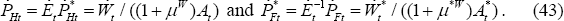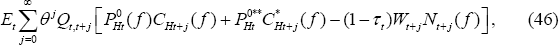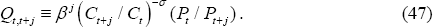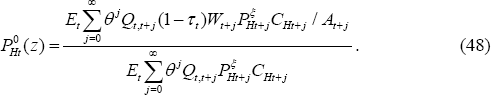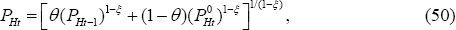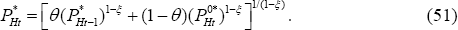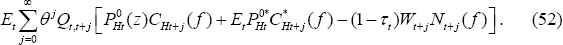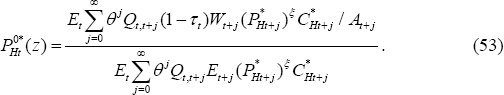RDP 2009-01: Currency Misalignments and Optimal Monetary Policy: A Re-examination 5. Price and Wage Setting

This section introduces the models of price and wage setting. Following CGG, wages are set flexibly by monopolistic suppliers of labour, but goods prices are sticky.

Wages adjust continuously, but households exploit their monopoly power by setting a wage that incorporates a mark-up over their utility cost of work.

Government is assumed to have only limited fiscal instruments. The government can set a constant output subsidy rate for monopolistic firms, which will achieve an efficient allocation in the non-stochastic steady state. But unfortunately, the markup charged by workers is time-varying because the elasticity of demand for their labour services is assumed to follow a stochastic process. These shocks are sometimes labeled ‘cost-push’ shocks, and give rise to the well-known trade-off in CGG's work between controlling inflation and achieving a zero output gap.

Households are monopolistic suppliers of their unique form of labour services. Household h faces demand for its labour services given by:

where

The first-order condition for household h's choice of labour supply is given by:

The optimal wage set by the household is a time-varying mark-up over the marginal disutility of work (expressed in consumption units).

Because all households are identical, W_t = W_t (h) and N_t = N_t(h).

Since all households are identical, Equation (37) implies:

Three different scenarios for firm behaviour are considered. In the first, prices can be adjusted freely. In the second – the PCP scenario that CGG analyse – firms set prices in their own country's currency and face a Calvo pricing technology. In the third, when firms are allowed to change prices according to the Calvo pricing rule, they set a price in their own currency for sales in their own country and a price in the other country's currency for exports. This is the LCP scenario.

The following notation is adopted. For any variable Z_t:

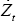• is the value under flexible prices.
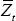• is the value of variables under globally efficient allocations. In other words, this is the value for variables if prices were flexible, and optimal subsidies to monopolistic suppliers of labour and monopolistic producers of goods were in place. This includes a time-varying subsidy to suppliers of labour to offset the time-varying mark-up in wages in Equation (37).
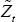• is the gap: the value of the variable under PCP or LCP relative to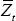

We will treat the PCP and LCP cases separately, so there will be no need to use notation to distinguish variables under PCP versus LCP.

5.1 Flexible Prices

Home firms maximise profits given by Equation (16), subject to the demand curve (10). They optimally set prices as a mark-up over marginal cost:

When optimal subsidies are in place:

From Equations (37), (39) and (40), it is apparent that the optimal subsidy satisfies

Note that from Equation (39) all flexible price firms are identical and set the same price. Because the demand functions of foreign residents have the same elasticity of demand for home goods as home residents, firms set the same price for sale abroad:

Equation (41), combined with Equation (38), implies:

So, it can be concluded that:

Because 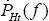is identical for all firms, Equation (23) collapses to

5.2 PCP

A standard Calvo pricing technology is assumed. A given firm may reset its prices with probability 1 – θ each period. Assume that when the firm resets its price, it will be able to reset its prices for sales in both markets. The PCP firm sets both prices in its own currency – that is, the home firm sets both P_Ht(f) and 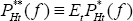in home currency. (As will become apparent, the firm optimally chooses the same price for both markets,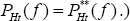

The firm's objective is to maximise its value. Its value is equal to the value of its entire stream of dividends, valued at state-contingent prices. Given Equation (11), it is apparent that the firm that selects its prices at time t, chooses its reset prices, 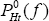and 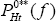, to maximise

subject to the sequence of demand curves given by Equation (10) and the corresponding foreign demand equation for home goods. In this equation, define

The solution for the optimal price for the home firm for sale in the home country is given by:

For sale in the foreign market, the optimal home currency price is:

Under the Calvo price-setting mechanism, a fraction θ of prices remain unchanged from the previous period. From Equation (7), we can write:

Taking Equations (48), (49), (50) and (51), it can be seen that the law of one price holds under PCP. That is, 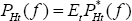for all f, hence 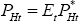. Hence, under PCP we have .

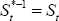5.3 LCP

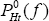The same environment as for the PCP case holds, with the sole exception that the firm sets its price for export in the importer's currency rather than its own currency when it is allowed to reset prices. The home firm, for example, sets in foreign currency. The firm that can reset its price at time t chooses its reset prices, and 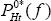, to maximise

The solution for 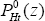is identical to Equation (48), while for export prices,

Equations (50) and (51) hold in the LCP case as well. However, the law of one price does not hold.

5.4 Subsidies

As in CGG, assume that subsidies to monopolists are not set at their optimal level except in steady state. That is, instead of the efficient subsidy given in Equation (41), we have:

Here, µ^W is the steady-state level of 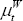. The time subscript on the subsidy rate τ has been dropped because it is not time-varying.