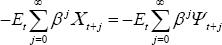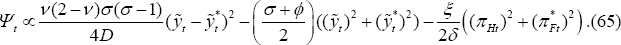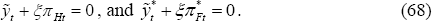RDP 2009-01: Currency Misalignments and Optimal Monetary Policy: A Re-examination 7. Optimal Policy under PCP
March 2009
- Download the Paper 512KB
As is familiar in the New Keynesian models with Calvo price adjustment, the loss function can be rewritten in the form:
where:
This loss function extends the one derived in CGG to the case of home bias in preferences, or non-traded goods (that is, v ≥ 1 rather than v = 1).
The policy-maker chooses values for 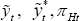 and
and  to minimise the loss, subject to the Phillips curves (55) and (56). Under discretion,
the policy-maker takes past values of
to minimise the loss, subject to the Phillips curves (55) and (56). Under discretion,
the policy-maker takes past values of 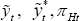 and
and  as given, and also
does not make plans for future values of these variables understanding that
future incarnations of the policy-maker can alter any given plan. The policy-maker
at time t cannot influence EtπHt+1
and
as given, and also
does not make plans for future values of these variables understanding that
future incarnations of the policy-maker can alter any given plan. The policy-maker
at time t cannot influence EtπHt+1
and 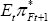 because future inflation levels are chosen by future policy-makers and there are
no endogenous state variables that can limit the paths of future inflation
levels. Hence, the policy-maker's problem is essentially a static one
– to maximise Equation (65) subject to Equations (55) and (56), taking
EtπHt+1
and
because future inflation levels are chosen by future policy-makers and there are
no endogenous state variables that can limit the paths of future inflation
levels. Hence, the policy-maker's problem is essentially a static one
– to maximise Equation (65) subject to Equations (55) and (56), taking
EtπHt+1
and 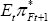 as given.
as given.
Even though home bias in consumption has been introduced, the optimal policy rules are the same as in CGG. The first-order conditions are given by:
These two ‘target criteria’ can be rewritten as:
The criteria given in Equation (68) are identical to those that arise in the closed economy version of this model. There is a trade-off between the goals of eliminating the output gap and driving inflation to zero, and the elasticity of substitution among goods produced in the country determines the weights given to output gaps and inflation.
It is worth emphasising that Equation (68) indicates the optimal policy entails a
trade-off between the output gap and the producer price inflation level. In a closed economy with no intermediate
goods, there is no distinction between producer and consumer prices. But in
an open economy there is an important distinction. The policies described
in Equation (68) imply that policy-makers should not give any weight to inflation
of imported goods. In conjunction with the Phillips curves, (55) and (56),
Equation (68) allows us to solve for the home and foreign output gaps and
πHt
and  as functions of current and expected future cost-push shocks, ut
and
as functions of current and expected future cost-push shocks, ut
and  .
With the output gap determined by optimal policy, the terms of trade must
adjust to ensure goods market clearing. But the terms of trade adjust freely
in the PCP world, because nominal exchange rate changes translate directly
into import price changes. In essence, the import sector is like a flexible-price
sector, so policy-makers can ignore inflation in that sector, as in Aoki (2001).
.
With the output gap determined by optimal policy, the terms of trade must
adjust to ensure goods market clearing. But the terms of trade adjust freely
in the PCP world, because nominal exchange rate changes translate directly
into import price changes. In essence, the import sector is like a flexible-price
sector, so policy-makers can ignore inflation in that sector, as in Aoki (2001).